It might be good just to pause here for a minute or two and get our bearings.  If you were deep in the woods with a compass, you could get to any point you want by simply knowing the direction you need to travel and how far you need to go in that direction.  On a grid, we could call the point where you are “the origin”, you are starting at the point (0, 0).

You also have a map with a grid and want to be able to draw a line on the map from where you are to your destination.  We are going to draw this line using the general line parametric equations for a line we have already discussed:

x = x₀ + D_x*S
y = y₀ + D_y*S

With the origin as your starting point (x₀, y₀) = (0,0).  Notice that I used different simpler notation that says

x₀ = 0 and
y₀ = 0.

This is called vector notation, instead of stacking the parametric equations on top of each other, we put them side by side in parenthesis and separate them with a comma (x, y). Using this vector notation I can rewrite both general parametric equations for a line as:

      (x, y) = (x₀, y₀) + (D_x, D_y)*S

A “vector” is expressed as two numbers written in parenthesis, separated by commas. In this case, the first number is the “x term” and the second number is the “y term”. When we “add” two vectors we add both “x terms” together and also both “y terms”.  When we multiply a vector times a number, then we just multiply both the “x term” and “y term” by that number.  And so, the “vector” equation for a line can be expanded like this:

   (x, y) = (x₀, y₀) + (D_x, D_y)*S
   (x, y) = (x₀, y₀) + (D_x*S, D_y*S)  (multiply the Direction vector by S)
   (x, y) = (x₀+D_x*S, y₀+D_y*S)        (add this to the starting point)

You can see how this last equation looks like the original stacked parametric equations, but they are written side by side in the parenthesis instead of one on top of the other.

This vector notation has an advantage, it is easier to write, and it lets us express the direction of the line on as (D_x, D_y). 

This becomes very helpful.

If you are in the deep woods, then it would be very helpful to convert your compass heading direction into this Direction vector and find (D_x, D_y) for your desired direction heading so you can draw the line on your “grid” map.

Since you set the origin (x₀, y₀) = (0, 0) to be where you are, the vector equation for the line to your destination is:

   (x, y) = (D_x, D_y)*S

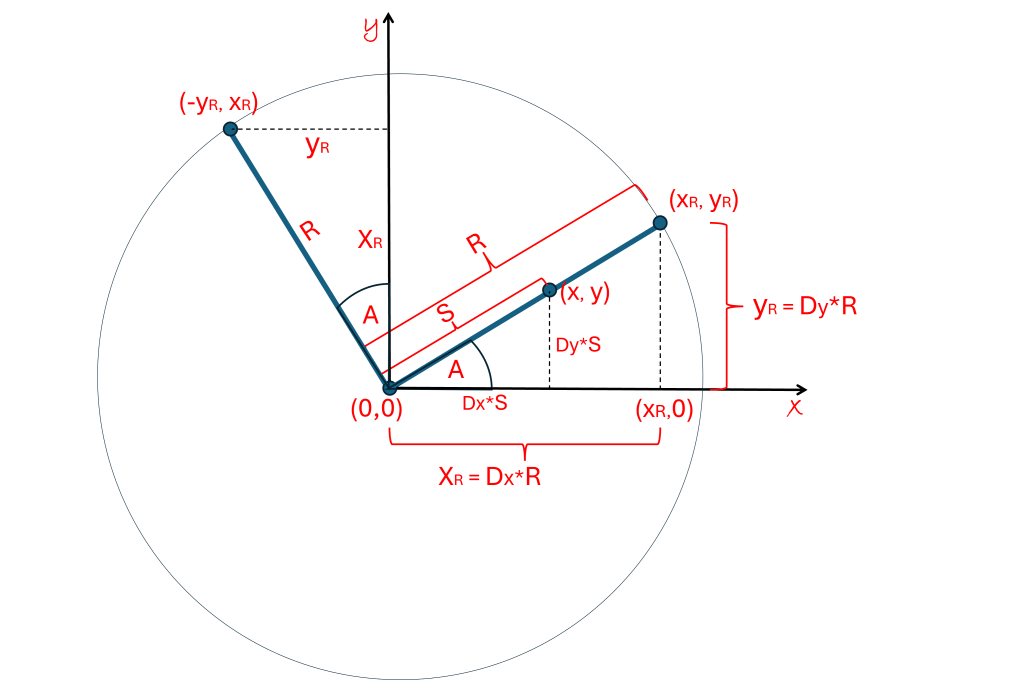
Now suppose that your destination is a distance “R” away from where you are. You can then draw a circle on your map with a radius “R” from the origin where you are.  You know that your destination is then somewhere on that circle.  You just need to know the direction (D_x, D_y) of your line to your destination point (see diagram above).

Let’s call the destination point (x_R, y_R).  Since we figure that the distance is “R”, then when S = R our vector equation is written:

(x_R, y_R) = (D_x, D_y)*R

And so using vector notation:

(D_x, D_y) = (x_R, y_R)/R = (x_R/R, y_R/R)

This tells us that if we know the point of our destination:

(x_R, y_R) and the distance R² = x_R² + y_R², then we can find the direction vector and draw our line on the map.  And if we only know the Angle “A” off the ‘x-axis’ from our compass, We can use our calculator and the definitions of Cos(A) = x_R/R and Sin(A) = x_R/R, to find the direction vector:

    (D_x, D_y) = (Cos(A), Sin(A))

Let us look at an example:  Suppose we knew that if we walked north 3 miles and then east 4 miles, we would reach our destination.  Then our destination is at (3 miles north, 4 miles east) on our map:

   (x_R, y_R) = (3, 4)  and R² = x_R² + y_R² = 3² + 4² = 25 or R = 5.

       So,

   (D_x, D_y) = (x_R, y_R)/R = (3/5, 4/5) North-east

       The line on the map could be drawn by using:

   (x, y) = (3/5, 4/5)*S    where S varies from 0 to R.

If we wanted to know the compass heading, then we could use the “inverse” Cos and Sin functions on our calculator to find the angle “A”:

   Cos(A) = 3/5   and Sin(A) = 4/5.

This might require a bit more knowledge of trigonometry.

Now we do something really interesting.  Suppose that we are still at the origin, facing directly at the point (x_R, y_R) but we want to find the point on the circle that is exactly 90 degrees to our left. If you look at the diagram, you will easily see that the point of destination would then be (-y_R, x_R).  The point directly behind us would be (-x_R, -y_R) and the point 90 degrees to the right would be (y_R, -x_R).

This is very useful if we want to draw lines that are perpendicular to the direction we are traveling along a line.  The direction (-D_y, D_x) is perpendicular to the left of the direction (D_x, D_y).