No matter where we turn our head in our 3-D world, we see the world projected on the 2-D “screen” in the back of our eyes.  These days, flat screens and cell phones are everywhere, they can display 2-D images on a flat surface that our brain interprets as being projections into a 3-D world.  From the last post, we are now equipped with math language to describe how this projection works.

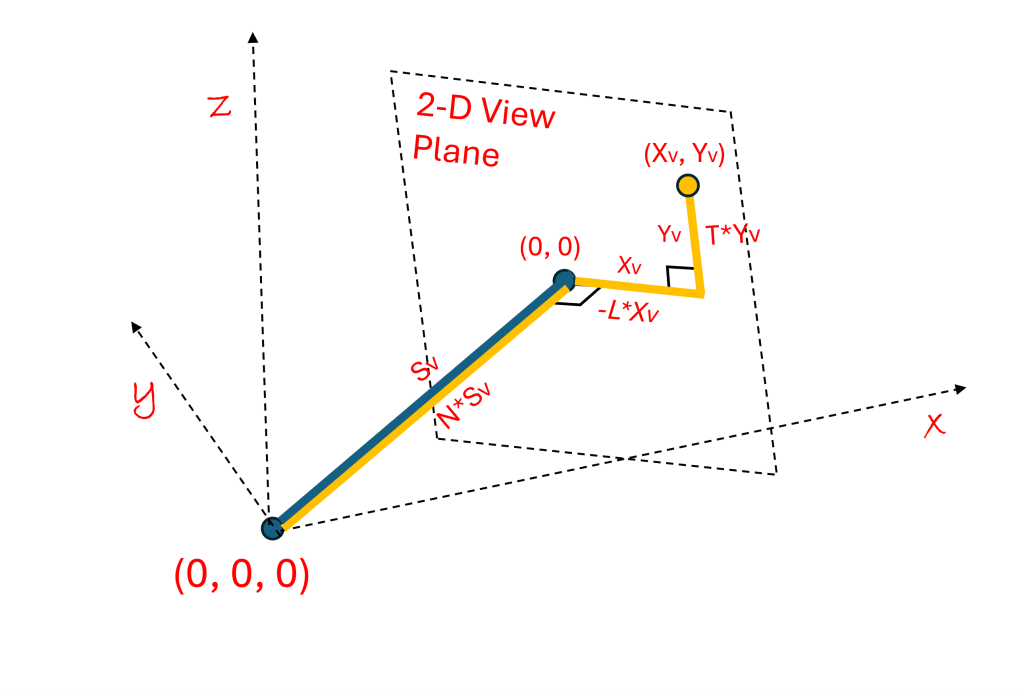
We can imagine that everything we see in front of our face is displayed on a big flat screen that is always a certain fixed distance in front of our nose and moves around with our head (it could be transparent).  Let’s call this screen the “View Plane” and say that it is always placed a fixed distance (S_V) perpendicular to our Nose direction (N).  This is not hard to imagine, I see lots of people carrying their cell phones around like this in front of their face all the time.

Your personal reference point (0, 0, 0), the origin, is always between your ears, the Nose direction (N), always points straight out in front of your face, the Left Ear direction (L) always points in the direction of your left ear, and the Top of head direction (T) always points through the top of your head.  This personal reference frame moves as you change the orientation of your head.

Since the View Plane in front of you is 2-D, every point on this screen can be located on a 2-D “x_v-y_v plane”.  Let’s draw such Cartesian coordinates on our View Plane. We choose the origin of the View Plane (0, 0) to be where our Nose direction (N) passes through the plane. We can choose the x_v-axis on the plane to point to the right (opposite the L direction), and then the y_v-axis would point in the Top of Head direction (T).

A single point (pixel) on this 2-D view screen (x_v, y_v), with a color (c_v), can also be located in the 3-D world.  Start at the origin (0, 0, 0), the middle of your head, then travel a distance S_v in the N direction to arrive at the origin of the View Plane (0, 0), then from there travel along the x_v-axis (in the negative L direction) a distance x_v, and then along the y_v-axis (in the T direction) a distance y_v.  From our orienteering days, we already know how find this 3-D point in math language:

    (x, y, z) = N*S_v + (-L)*x_v + T*y_v
                   = [N, L, T]^.(S_v,-x_v,y_v)

And so, we can find the 3-D coordinates for any point on the 2-D View screen (x_v, y_v) when we know the distance to the view screen (S_v) and the orientation of the head (N).  In review, the middle of the head is always at the origin (0, 0, 0) and you are looking in the Nose direction N:(D_x, D_y, D_z) in the 3-D world, the direction vectors of the head reference frame are:

         N = (D_x, D_y, D_z)
         L = (-D_y/D_r, D_x/D_r, 0)
         T = (-D_x*D_z/D_r, -D_y*D_z/D_r, D_r)

         D_r² = D_x² + D_y²

In the Cartesian frame of the 3-D world around us the orientation of our head can be determined by two angles (A_xy and A_z).  As you remember, A_xy is the angle we have rotated our head left or right in the x-axis in the x-y plane, and A_z is the angle that we have tilted our head up or down off the x-y plane.  In review, the direction vector of the head is found from the following:

       D_x = Cos(A_xy)*Cos(A_z)
       D_y = Sin(A_xy)*Cos(A_z)
       D_z = Sin(A_z)

The dot products of the [N, L, T] head reference vectors are:

   N^.N = L^.L = T^.T = 1
   N^.L = N^.T = L^.T = 0

since they are all perpendicular to each other.
We also find that:

     N^.(x, y, z) = N^.( N*S_v + L*(-x_v) + T*y_v )
                        = N^.N*S_v + N^.L*(-x_v) + N^.T*y_v
                        = 1*S_v + 0*(-x_v) + 0*y_v
                        = S_v

     L^.(x, y, z) = L^.( N*S_v + L*(-x_v) + T*y_v )
                        = L^.N*S_v + L^.L*(-x_v) + L^.T*y_v
                        = 0*S_v + 1*(-x_v) + 0*y_v
                        = -x_v

     T^.(x, y, z) = T^.( N*S_v + L*(-x_v) + T*y_v )
                        = T^.N*S_v + T^.L*(-x_v) + T^.T*y_v
                        = 0*S_v + 0*(-x_v) + 1*y_v
                        = y_v

Another way of writing these stacked equations with dot products is simply:

      [N, L, T].(x, y, z) = (S_v, -x_v, y_v)

So, we can see that with this miracle matrix [N, L, T] can map a point in 3-D space onto a point (x_v, y_v) on a View Plane that is a distance S_v away.

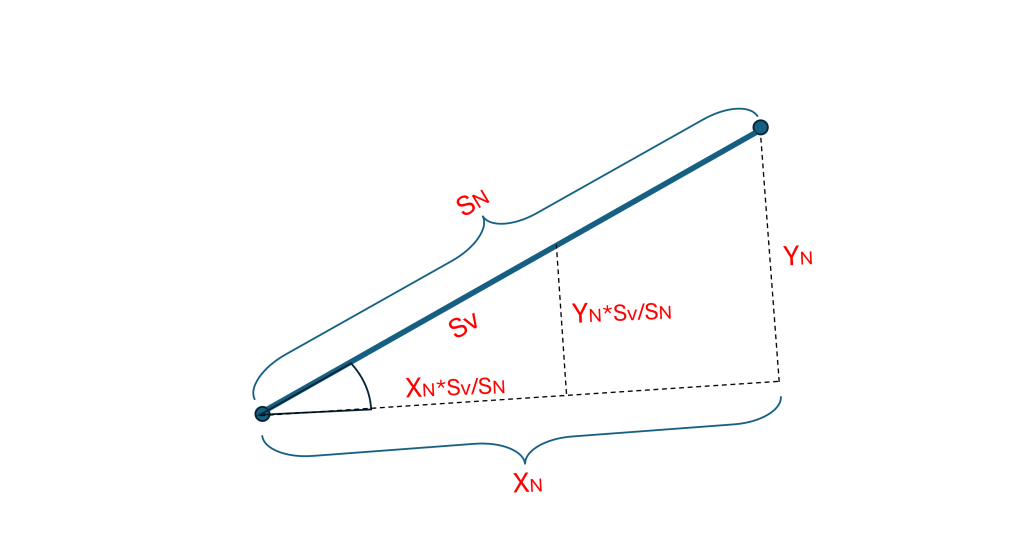
Let’s finish this idea off.  Suppose we have any point in 3-D space (x, y, z), then

[N, L, T]^.(x, y, z) = (S_N, -x_N, y_N)

maps (x, y, z) onto a point (x_N, y_N) on 2-D view plane that is a distance S_N away from your nose.  Using simple geometry, this point can be mapped onto a point (x_v, y_v) in any parallel View Plane that is a distance S_v away by using:

    (x_v, y_v) = (x_N, y_N)*S_v/S_N

And so, we can map a 3-D world onto a 2-D view plane.  Our brain perceives these 2-D images from colored points (pixels) from our flat screens as 3-D images.