We can navigate in 3-D to any point (x_R, y_R, z_R), in Cartesian Coordinates, by starting at the origin (0, 0, 0) and in the 2-D, x-y plane, walking in the x-direction (1, 0, 0) a distance x_R, then turning left 90 degrees and walking a distance y_R in the y-direction (0, 1, 0), still on the x-y plane.  This is the same as we did in 2-D except we put an extra ‘0’ in the third ‘z’ direction.  At this point we are still on the x-y plane at the point (x_R, y_R, 0).  The z-direction is straight up, so we would now need a ladder to climb up or a shovel to dig down, it is helpful to pretend we can fly (or dig).  From this point (x_R, y_R, 0) on the x-y “ground” plane, we fly straight up in the z-direction (0, 0, 1) a distance z_R, and we successfully arrive at the point (x_R, y_R, z_R).

We can express this journey with vectors, as we did in 2-D, by connecting (adding) lines together to form the path:

   (x_R, y_R, z_R) = (1, 0, 0)*x_R + (0, 1, 0)*y_R + (0, 0, 1)*z_R
                        = (x_R, 0, 0) + (0, y_R, 0) + (0, 0, z_R)
                        = (x_R, y_R, z_R)

        And using dot product notation, this can be written:

   (x_R, y_R, z_R) = (1, 0, 0)*x_R + (0, 1, 0)*y_R + (0, 0, 1)*z_R
                        = [(1, 0, 0), (0, 1, 0), (0, 0, 1)]^.(x_R, y_R, z_R)

The [(1, 0, 0), (0, 1, 0), (0, 0, 1)] matrix is called the identity matrix.

We could also arrive faster by flying along a straight line connecting the two. Fly along a direction (D_x, D_y, D_z), from the origin directly to this point, (x_R, y_R, z_R) a distance “R” away:

   (x_R, y_R, z_R) = (D_x, D_y, D_z)*R

        Where the distance ‘R’ is found by:

    R² = x_R² + y_R² + z_R²

From the equation above for this line, we can easily find the direction vector from the origin to any point (x_R, y_R, z_R), similar to what we did in 2-D.

      (D_x, D_y, D_z) = (x_R/R, y_R/R, z_R/R)

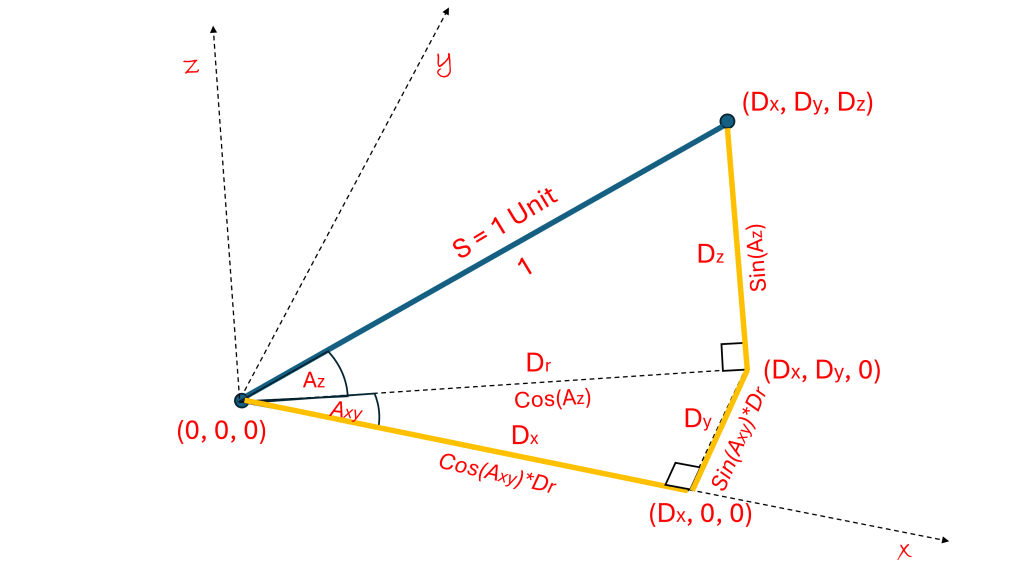
Recall that the direction vector always has a distance of 1 unit, as seen in the diagram above.  In the diagram, we have attempted to show a 3-D path on a 2-D piece of paper.  Note that in the diagram, D_r is the distance from the origin to the point (D_x, D_y, 0) in the x-y plane. From the Pythagorean theorem, we find that the length:

      D_r² = D_x² + D_y²    and
      D_r² + D_z² = 1        thus combining these
      D_x² + D_y² + D_z² = 1.

The total length of the distance vector is 1 unit, as required.  Everything is consistent.  Now we use the definition of the ‘Sin’ and ‘Cos’ and can see, from the diagram above, that:

     Cos(A_xy) = D_x/D_r
     Sin(A_xy) = D_y/D_r

      Cos(A_z) = D_r/1
      Sin(A_z) = D_z/1

    Thus

       D_x = Cos(A_xy)*D_r = Cos(A_xy)*Cos(A_z)
       D_y = Sin(A_xy)*D_r = Sin(A_xy)*Cos(A_z)
       D_z = Sin(A_z)

And so, if we stand at the origin facing in the x-direction, and rotate our “head” an angle A_xy to the left, and then tilt our head an angle A_z off the x-y plane to look directly at the point (x_R, y_R, z_R), we can find the direction vector pointing to this point using these angles:

   (D_x, D_y, D_z) = (Cos(A_xy)*Cos(A_z), Sin(A_xy)*Cos(A_z), Sin(A_z))

       And then draw the line to this point:

    (x_R, y_R, z_R) = (D_x, D_y, D_z)*R

Now that we are staring at a point in the sky, with our nose pointed directly at the point, we can ask about “reference frame” of our head.  What direction is our left ear pointing, for example.  Our left ear is pointing in the direction, still in the x-y plane, that is 90 to the left of the A_xy angle we rotated our head (-D_y/D_r, D_x/D_r, 0). We divide by D_r because in 3-D we must make the length of the direction vector equal to 1.  If this seems vague, look back and review how to find 90 degree directions in the 2-D plane in the top diagram taken from previous posts.

When we tilt our head, we can ask what is the direction that the top of our head points, 90 degrees up from the angle A_z. It perhaps takes a bit more imagination to see this, since we are facing in the x-y plane (D_x/D_r, D_y/D_r, 0) and have tilted our head up to look at D_z, we find that the “shadow” of our head is pointed behind us, in the x-y plane (-D_x/D_r, -D_y/D_r, 0), then looking at the elevation D_r (when rotated 90 degrees) we find that (-D_x*D_z/D_r, -D_y*D_z/D_r, D_r) is the direction of the top of our head.  So, in the reference frame of our head:

     Direction of our Nose:     (D_x, D_y, D_z)
     Direction of Left ear:         (-D_y/D_r, D_x/D_r, 0)
     Direction of Top of head:  (-D_x*D_z/D_r, -D_y*D_z/D_r, D_r)

Let us verify that these direction vectors all have a length of 1.  The Nose direction we have verified.  For the Left ear direction:

    L^.L = (-D_y/D_r)² + (D_x/D_r)² + 0² = (D_y² + D_x²)/D_r² = 1

For the Top of head direction:

    T^.T = (-D_x*D_z/D_r)² + (-D_y*D_z/D_r)² + D_r² = (D_y² + D_x²)*D_z²/D_r² + D_r²
                                                                    = D_z² + D_r² = 1

Now let’s find what happens when we find the dot product of these direction vectors, we will call them the N, L, and T directions respectively.

N^.N = (D_x, D_y, D_z)^.(D_x, D_y, D_z) = D_x² + D_y² + D_z² = 1

N^.L = (D_x, D_y, D_z)^.(-D_y/D_r, D_x/D_r, 0) = -D_x*D_y/D_r + D_y*D_x/D_r + 0
                                                                  = 0

N^.T = (D_x, D_y, D_z)^.(-D_x*D_z/D_r, -D_y*D_z/D_r, D_r)
        = -D_x²*D_z/D_r + -D_y²*D_z/D_r + D_z*D_r
        = -(D_x² + D_y²)*D_z/D_r + D_z*D_r
        = -D_r²*D_z/D_r + D_z*D_r
        = 0

L^.T = (-D_y/D_r, D_x/D_r, 0)^.( -D_x*D_z/D_r, -D_y*D_z/D_r, D_r)
       = D_y*D_x*D_z/D_r² + -D_x*D_y*D_z/D_r² + 0
       = 0

We also verified that L^.L = 1 and T^.T = 1 above.  So, in general, if we dot any of these N, L, T direction vectors with themselves, we get ‘1’, but if we dot any of them with each other, we get ‘0’.  It turns out that this is a requirement for any three perpendicular direction vectors in a 3-D Cartesian reference frame.  I find the “head” reference frame to be more natural because we can relate to it better, so I use this reference frame for whatever direction I am looking.  It is also a great reference frame for video games.

We have already seen from perpendicular 2-D paths how we can convert between a reference frame to our “ground” x-y-z reference frame.  To understand this, let’s take a journey: Fly in the Nose direction a distance S_N, then fly in the Left ear direction a distance S_L, and then in the Top of head direction a distance S_T.  Then we will arrive at the point:

    (x, y, z) = N*S_N + L*S_L + T*S_T

       or in dot product notation:

     (x, y, z) = [N, L, T]^.(S_N, S_L, S_T)

This amazing equation lets you convert any point in your “head frame” of reference (S_N, S_L, S_T), when your head is pointing in your Nose direction N:(D_x, D_y, D_z), to a point in the “ground” frame (x, y, z).  You might also want to do this the other way around.  Review how we did this in 2-D, by “dotting” each side by each of the direction vectors, we get:

    (S_N, S_L, S_T) = [N, L, T]^.(x, y, z)

This is how video games convert a 3-D world, stored in “ground” (x, y, z) coordinates, into the perspective of the viewer’s head (S_N, S_L, S_T) coordinates.  The details need to be worked out but using this equation we can map a 3-D world onto a 2-D screen in the viewer’s perspective, no matter the relative direction of the viewer’s head.  We will stop here, there is a lot to take in.