Tag Archives: philosophy

Math Moments – Distance is Relative in Space-Time

This diagram is here as a reminder to read and understand the previous post.

It is obvious that because the speed of light is constant in every possible reference frame, then it requires distances and times to be different between events relative to the reference frame in which we measure them. So, if distances change from one reference frame to another, then how exactly do we make sense of the concept of distance in Space-Time?

We have seen in 3-D space, when a point (x, y, z) is not moving in time, we simply change our reference frame by “moving our head”. We can set our Nose direction to point directly toward the point (x, y, z), in the direction (Dx, Dy, Dz). Recall that the point:

     (x, y, z) = (Dx, Dy, Dz) * S

where S is the distance from our nose (0, 0, 0) to the point (x, y, z). We assume that rotating our head does not change the distance to the point.  This is what is called a “spherical metric”.

It is easier to picture this in 2-dimensions (when z = 0), so we will use only the ‘x’ and ‘y’ dimensions for our illustration. Recall:

    (x, y) = (Dx, Dy) * S

      meaning

      x = Dx * S
      y = Dy * S

Where the (Dx, Dy) direction is shown in the following diagram:

Recall that if we “dot” (x, y) with the direction (Dx, Dy):

   (Dx, Dy).(x, y) = (Dx, Dy).(Dx, Dy) * S
                             = (Dx*Dx + Dy*Dy) * S
                             = (Dx2 + Dy2) * S

If the metric (Dx2 + Dy2) = 1, then the Distance (S) is just this dot product.  We have looked at this in detail before.  This is called a “spherical” metric, because distances are the same in all directions, like the radius of a sphere.  With this metric, the distance is the same regardless of the orientation (angle) of the reference frame. Nothing new here.

Yet if the point (x, y, z, C*t) in Space-Time is moving, then the situation is different.  We cannot set a fixed “Nose direction” to look at a moving point.  We first must start moving with the same speed in the same direction as the point.  Now in this moving reference frame, the point is stationary, not moving, and then the “Nose Direction” can be set.

In space-time, the speed at which a point is moving is determined by the angle (At) it is off the C*t-axis. Going into another frame of reference means finding the “angle” of a line that will match the point’s speed. The angle At is often called the “boost” parameter and is directly related to the speed of the point traveling along this line. We will look at how to change the speeds (At) of reference frames relative to each other in space-time.

We can use the same concepts to find the meaning of Distance in Space-Time.  Consider the example of a moving flash bulb (bulb frame) between two stationary mirrors (mirror frame) that we examined in the last post.  For simplicity and clarity, we are only looking at the ‘x’ and ‘C*t’ dimensions and have put in grid lines parallel to the “x-axis” and “C*t-axis”.  Here the x-axis points in the same direction that the bulb is moving.

This does not restrict us because we always can rotate our frame of reference so that the ‘x’ direction is pointing in the same direction that the point is moving, we are ignoring the y = 0 and z = 0 coordinates.  Now as before, let’s look at the same events in the perspective of the “bulb frame”, with the “xb-axis” and “C*tb-axis” defining this frame.  In the following diagram we mark in the same “grid lines” parallel to the x-axis and C*t-axis, but now in the viewpoint of the “bulb” frame.

As we mentioned before, the grid lines in the mirror frame are not mutually perpendicular when seen in the bulb frame, they are stretched out “diamonds”.  Note however that the “light lines” (yellow) in both frames of reference fall along the same points (they are 45 degree lines in both frames of reference).  Another thing to note is that the angle (At) of the bulb from the C*t-axis to the C*tb-axis is the same as the angle (At) between the negative-x-axis and the negative-xb-axis, but unlike the spherical rotations, they are now rotating in opposite directions and squeezing closer together.

As the angle (At) is increased, the two “mirror” axes, as seen from the “bulb” frame of reference, would come closer together, squeezing the “mirror” reference grid together like one of those fold-out books, until they get to 45 degrees (the speed of light), where the mirror frame axii are completely squeezed together and the grid lines disappear completely. Stare at the diagram above and you might be able to imagine it. This might seem really weird at first, but it is a consequence of the speed of light being the same (at 45 degrees) in both frames.

What do you think the “bulb” frame of reference would look like in the “mirror” frame of reference?  See the diagram below:

Let’s now see if the math works out.  Let us look at a specific point (x, C*t) in the mirror frame and ask how it would look in the bulb frame. First let’s write the equation for the “C*tb” axis as seen in the mirror frame.  Let’s say it is in the direction (Dx, Dt). Recall that this is the same direction as the “bulb” world line is in the above world diagram. Then any point (xtb, C*ttb) at a distance St along the C*tb-axis can be written:

   (xtb, C*ttb) = (Dx, Dt)*St

Where (Dx, Dt) marks the direction of the bulb world line in the mirror frame, and St is a distance marked along the C*tb-axis, and is yet to be determined.  We can also find the equation of a point along the xb-axis in the mirror frame.

    (xxb, C*txb) = (Dt, Dx)*Sx

Note that (Dt, Dx) is the direction of the xb-axis which is at the same angle, At, above the x-axis (as required by the space-time geometry) and Sx is the (yet undetermined) distance marked along the xb-axis.

From our orienteering days, we have seen that we can arrive at the point (x, C*t) by “moving” along the C*tb-axis a distance St, and then turning right to “move” in the direction parallel to the xb-axis a distance Sx (as seen by the green lines in the diagram).  Note that the Sx and St are the coordinates in the “bulb frame” of reference. And so:

    (x, C*t) = (Dx, Dt)*St + (Dt, Dx)*Sx

We can now “dot” both sides with a direction that is perpendicular to the C*tb-axis (Dt, -Dx) to eliminate the St term and thus find Sx:

 (Dt, -Dx).(x, C*t) = (Dt, -Dx).(Dx, Dt)*St + (Dt, -Dx).(Dt, Dx)*Sx
                                =(Dt*Dx + –Dx, Dt)*St  + (Dt*Dt – Dx*Dx)*Sx
                                = 0*St + (Dt2 – Dx2)*Sx
                                = (Dt2 – Dx2)*Sx

and we can find the St coordinate by a similar process:

 (-Dx, Dt).(x, C*t) = (-Dx, Dt).(Dx, Dt)*St + (-Dx, Dt).(Dt, Dx)*Sx
                                =(-Dx*Dx + Dt, Dt)*St  + (-Dx*Dt + Dt*Dx)*Sx
                                = (Dt2 – Dx2)*St + 0*Sx
                                = (Dt2 – Dx2)*St

If we define the metric such that

        Dt2 – Dx2 = 1,

(called a hyperbolic metric) then the “magic” matrix that transforms the event (x, C*t) into the (Sx, St) event coordinates in the “bulb frame” is found by combining the three equations above in a matrix equation, as usual:

     [(Dt, -Dx), (-Dx, Dt)].(x, C*t) = (Sx, St)

And there we have it, the way to convert between the two frames of reference, this is also referred to as the “Lawrentz Transform”.

We should say a few words about the meaning of the hyperbolic metric Dt2 – Dx2 = 1.  If we draw a plot of this metric, we can see that Dx, and Dt are defined by coordinates of points on the unit hyperbola as shown:

There are special functions, the hyperbolic sine (Sinh) and cosine (Cosh), that are defined to find (Dx, Dt) from the angle At:

   (Dx, Dt) = (Sinh(At), Cosh(At))

We see that this is a new way of defining distances in Space-Time.  If the point (x, C*t), is in the direction (Dsx, Dst):

           (x, C*t) = (Dsx, Dst)*S   (where S is the spacetime distance)
then   1 = Dst2 – Dsx2
           S2 = S2*(Dst2 – Dsx2)
           S2 = (S*Dst)2 – (S*Dsx)2
           S2 = (C*t)2 – (x)2

And we have found a way to define distance in space-time.

Returning to our moving bulb example, we finish off by finding the direction (Dx, Dt) of the bulb, moving with a speed “v” in the“positive-x-direction” in space-time (which is also the direction of the “C*tb” axis in the mirror frame).  After a time ‘tb’, the bulb has traveled a distance of xb = v*tb thus:

   (v*tb, C*tb) = (Dx, Dt) * St

Where St is the space-time distance traveled by the bulb, which we now know to be:

    St2 = (C*tb)2 – (v*tb)2
          = (C2 – v2)*tb2

And so

St = Sqrt(C2 – v2)*tb

   And thus we have found:

Dx = v/Sqrt(C2 – v2)
Dt = C/Sqrt(C2 – v2)

Finally we have come full circle and filled in the unknowns.  Don’t worry if you are having trouble understanding it all. It still takes me a bit of time to completely wrap my mind around these concepts.  Just for reference, in science literature, Dt is often called the Greek letter “gamma” and the ratio ‘v/c’ is often called “beta”, thus Dx = gamma*beta and Dt = gamma.

I believe that that is sufficient for now. You might have many questions, but if you read and study this post a few times, you will be able to get the gist of how Special Relativity works to transform between Space-Time reference frames.

Standard

Math Moments – Special Relativity

So far, we have been thinking of the time (C*t) dimension to be just another dimension in space, completely symmetric with the other three directions (x, y, z), yet we have already seen a problem with this concept.  The reasonable concept of time requires that a point cannot travel everywhere with infinite speed and be everywhere at the same time. Einstein postulated that the speed of light is the speed limit that prevents everything from happening all at once.  This concept creates limitations on the “time direction” (Dt) and even affects the “symmetric” geometry of space-time.

Let us look at a simple example that illustrates this concept.  In space-time, every point (x, y, z, C*t) is called an “event” with a position in space and in time.  Let us consider a flash bulb traveling in the positive ‘x’ direction with speed “v”.  When the bulb is exactly between two mirrors, it flashes.  We can call this flash our reference event, (0, 0, 0, 0).  Let us suppose that the two stationary mirrors are on both sides of the flash bulb, so that when the bulb flashes, the space-time coordinates of the two mirrors are (-xm, 0, 0, 0) and (xm, 0, 0, 0) respectively, where xm is the distance to each of the mirrors.  See the diagram below.  It is assumed that the light from the flash will propagate out in all directions (in a perfect sphere) at the speed of light.

It is simple to predict what will happen as time passes, the light from the flash will travel at the speed of light toward both mirrors. Since we assume by symmetry that the speed of light traveling in the positive ‘x’ direction is the same speed that it travels in the negative ‘x’ we imagine that it will arrive at both mirrors at the same time, tm, and then reflect back toward the center.  The diagram below is called the “world diagram” in the reference frame of the mirrors, it maps out what will happen at any time “t” in the future.  In this diagram we only show the ‘x’ axis, for simplicity, describing only what happens in the ‘x-direction’, which is plotted against the ‘C*t’ axis that shows what will happen in time.

In this diagram, the flash of light follows the yellow “light line” (where x = C*t in the ‘positive-x-direction’ and x = -C*t in the ‘negative-x-direction’).  In this diagram, then, Light lines always travel at a 45-degree angle off the ‘C*t’ axis.  Anything that is traveling at a speed slower than light (everything else) travels at an angle less than 45 degrees off the ‘C*t’ axis.  For example, the flash bulb that is traveling with a speed ‘v’ in the positive x-direction on this diagram travels along its green world line (x = v*t) and, of course, ‘v’ is less than ‘C’. In this diagram, the lines tell you where everything will be at any time ‘t’ in the future.

The world line for the mirrors, for example, go ‘straight up’, the mirrors do not move in space, they start at -xm and xm and just travel through time along the ‘C*t’ axis.  From the above diagram, can you see everything that will happen?  The light will hit both mirrors at the same time ‘tm’ and bounce back. The flash bulb will just keep moving off in the x-direction, and the mirrors will just stay where they are.  Staring at the diagram you can see it all.  You might even see that the flash bulb will flash again, when the light bouncing back off the mirror hits it.

The events are labeled on the diagram, the flash is at the origin, light bounces off the mirror in the positive direction at ‘O+’ and simultaneously bounces of the mirror in the negative direction at ‘O–‘,  ‘O’ is the midpoint between O+ and O–, and ‘P’ is when the light comes back to center.

Things start getting a bit weird, however, if you are looking at the world in the reference frame of the flash bulb.  In this frame of reference (you are traveling along with the bulb), the flash bulb is not moving, yet the two mirrors are moving at a relative speed ‘v’ in the negative-x-direction.  As before, the flash is triggered when the bulb is exactly in the mid-point between the mirrors.

In this reference frame, the moving mirrors are certainly not going to change the velocity of light, you will still see the light propagating outward in a perfect sphere at a 45 degree angle in your world diagram.  There is an obvious difference, however. You observe the light bouncing off the mirror that is traveling toward you (O+) before it bounces off the mirror that is traveling away from you (O–), the distances are different.  Please refer to the diagram above. In the frame of the flash bulb, the events O+ and O– do not happen at the same time.

How can this be? In the first case, the reference frame of the mirrors, the light bounces off both mirrors at exactly the same time, but in the frame of reference of the flash bulb, the light bounces off the approaching mirror first before it bounces off the receding one.  Which observation is right? Looking at the two world diagrams of each case, it is obvious that one diagram is not a simple rotation of the other.  Distances and directions have changed when the relative velocities change.  Lines between events that are perpendicular in one frame of reference are not perpendicular in the other.

So, we see that if there does exist a uniform speed limit ‘C’ in all frames of reference, that is the same regardless of direction or speed of the observer, then events that are simultaneous in one frame, must happen at different times in another, and the angles and distances observed between events in the space-time diagram must change from one reference frame to another.  This concept is what was going through the mind of Albert Einstein when he formulated the theory of Special Relativity.

In order for the math to work, to predict what will be observed in one reference frame from the perspective of the other, we find that the symmetry or “geometry” of space-time cannot be spherical and distances are not preserved between different “rotations” or frames of reference.  For spherical symmetry and geometry, Dx2 + Dy2 + Dz2 + Dt2 = 1 is true for all directions and times.

We now are starting to see that this doesn’t work in real space-time, where the speed of light is constant in all frames of reference and rotations of world lines cannot exceed 45 degrees off the ‘C*t’ axis.  There is a geometry that does allow this all to happen, it is called “hyperbolic” geometry where distances are measured as Dx2 + Dy2 + Dz2 – Dt2 and vary by the velocity of one frame of reference relative to another.  Mathematically, this is the true working version of space-time and is called Minkowski Space.  The math has been meticulously worked out. We will cover some of the details later. The interesting thing is that through more than a century of observations, the Theory of Special Relativity has been proven time and time again.  Scientists have still not been able to find an exception.  It is used in everything from GPS, to positioning of satellites, to radioactive decay of cosmic particles.  It works! But it takes a bit of getting used to.  Space and time are inextricably connected.

Standard

Math Moments – Finding Directions in 4-D

As we enter dimensions beyond our physical experience, it might help our understanding to look back and see patterns in smaller dimensions that still apply in larger dimensions.  Is there such a pattern when finding directions (Dx, Dy, Dz, Dt) in 4 dimensions or larger.  One obvious pattern, as dimensions increase, is the way we measure distance:

   1-D:         Dx2 = 1
   2-D:         Dx2 + Dy2 = 1
   3-D:          Dx2 + Dy2 + Dz2 = 1
   4-D:          Dx2 + Dy2 + Dz2 + Dt2 = 1

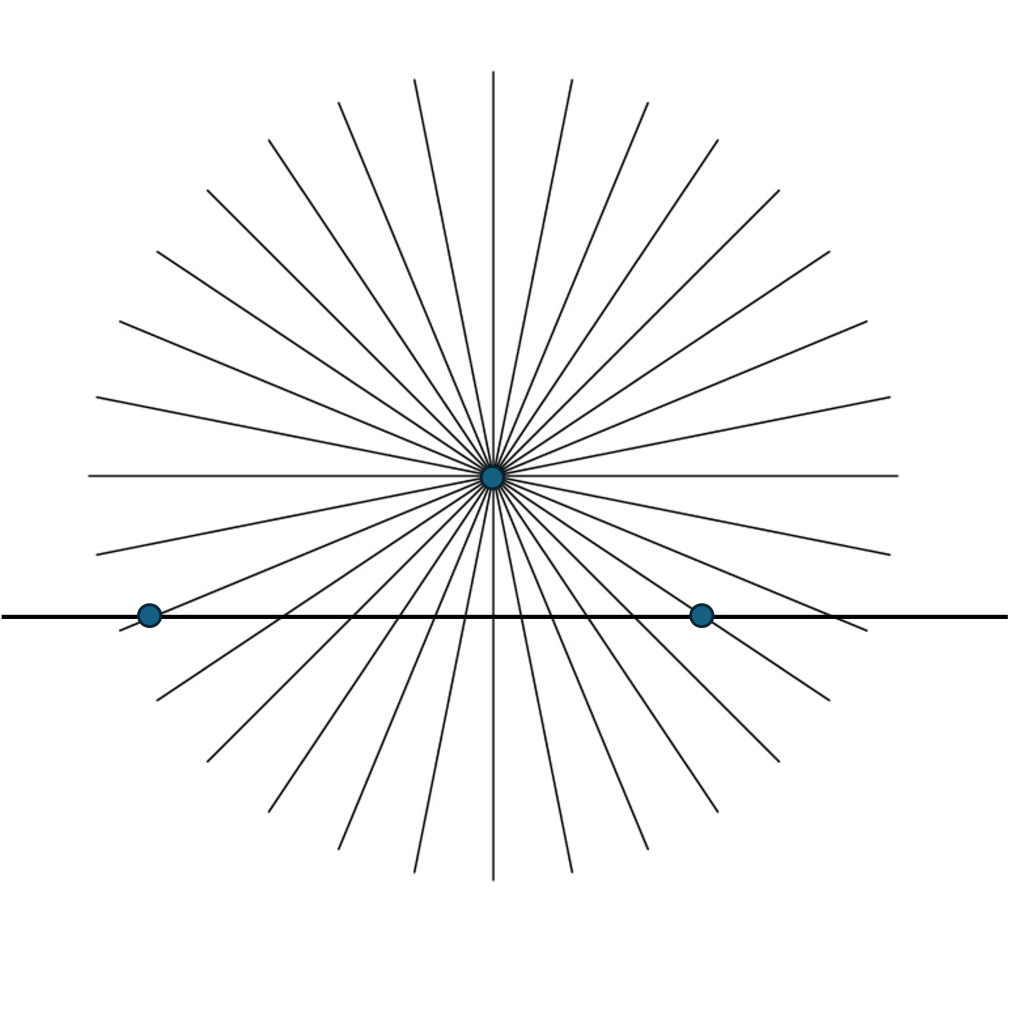
The pattern for higher dimensions is obvious. We expect this pattern to continue to any number of dimensions; we just keep adding on perpendicular triangles.  See the diagram above.

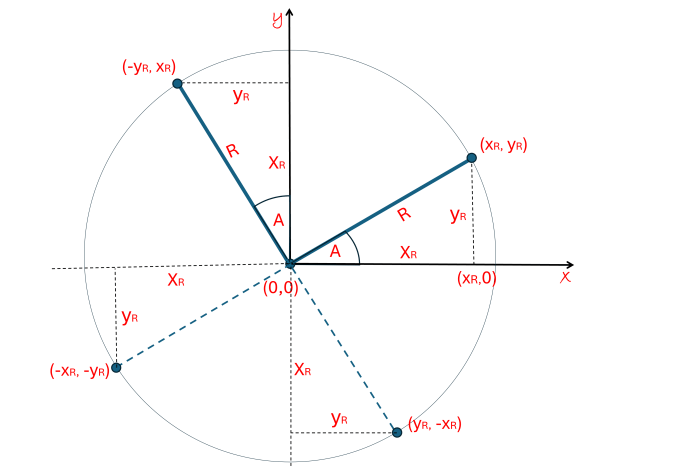
There is one problem with setting directions in higher dimensions that is not so obvious. For example, in 1-D, Dx2 = 1 means that Dx = 1 or Dx = -1, this defines the directions to be along the positive or negative x-axis.  So far so good. In 2-D, however, when Dy2 = 1, it forces Dx2 = 0, which does not indicate either a positive or negative direction along the x-axis.  This ambiguity is due to the rotational symmetry of perpendicular lines, as we have mentioned before, you can “flip” negative and positive directions around a perpendicular direction, and nothing changes.

This ambiguity of direction exists whenever we add a new dimension.  In 3-D, for example, when Dz2 = 1, it forces Dx2 + Dy2 = 0 and there are ambiguities as to where to place the direction of both the x-axis and y-axis.  To a man standing exactly on the north pole, for example, every direction is south, there is no east and west.  I have also heard it said that no matter how you comb the fuzz flat on a tennis ball, there will always be a part (singularity).

To deal with these ambiguities when any of our direction parameters is zero, it is helpful to fix the angles of the x-axis, y-axis, z-axis, etc. so that directions will not be ambiguous when you pass through the “singularities” where one or more of the direction parameters are forced to be zero.  So a man standing on the north pole, where every direction is south, still knows which angle to face if he wants to point to Paris, France.  This makes defining directions consistent.

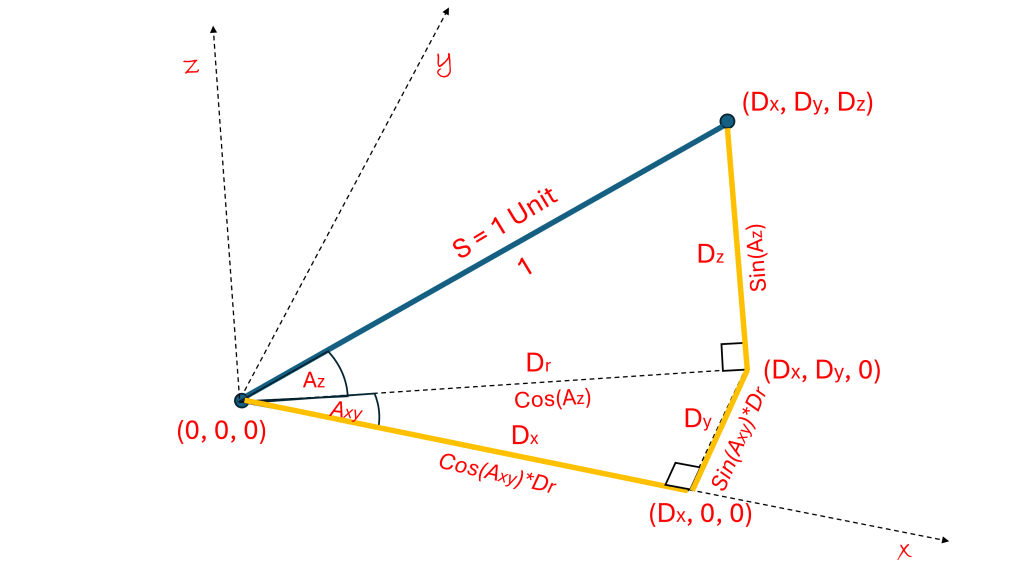
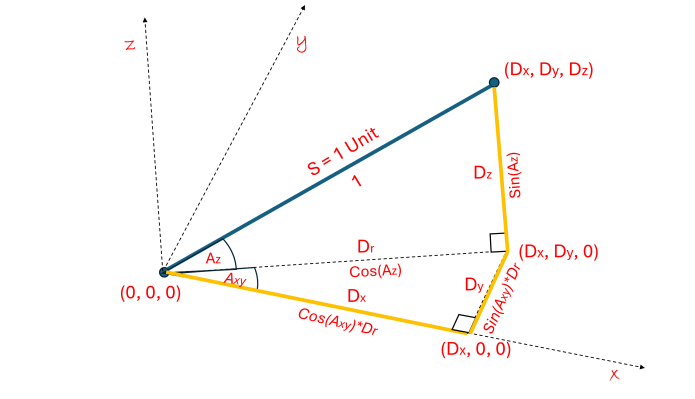
Let us look at a way to define directions as we are increasing dimensions. We defined the angle Axy to be the angle from the x-axis in the x-y plane.  Then we defined the angle Az to be the angle off of the x-y plane in the z direction.  Listing the direction parameters for the dimensions we know:

   2D: D2 = (D2x, D2y) = (Cos(Axy), Sin(Axy))
   3D: D3 = (D3x, D3y, D3z) = (D2x*Cos(Az), D2y*Cos(Az), Sin(Az))
                 = (D2x, D2y, 0)*Cos(Az) + (0, 0, 1)*Sin(Az)

We added the “2” and “3” subscripts to indicate the dimension.

It might take you a few minutes to see the pattern.  Expanding into 4-D, we define the angle At to be the angle off the x-y-z space toward the t-axis, then continuing the pattern, the direction in 4-D is:

    D4 = (D4x, D4y, D4z, D4t) = (D3x, D3y, D3z, 0)*Cos(At) + (0, 0, 0, 1)*Sin(At)

    So putting them together and stacking them we get:

         D4x = Cos(Axy)*Cos(Az)*Cos(At)
         D4y = Sin(Axy)*Cos(Az)*Cos(At)
         D4z =                   Sin(Az)*Cos(At)
         D4t =                                   Sin(At)

And we have found the Direction parameters in 4-D, and hopefully we can see the pattern that will allow us to use the same scheme to find directions in any dimension. An interesting side note: The angle in the t-direction, At, determines how close the 4-D direction is to the t-axis. When it gets close to 90 degrees, the direction is close to the t-axis and Cos(At) is close to zero, and D4x, D4y and D4z are close to zero, this restricts motion in the x-y-z space. The faster time is moving, the more restricted the motion is in 3-D space. How strange. We will see just how strange in the following post.

Standard

Math Moments – Does Space-Time Exist?

We are now ready to expand our 3-D space into 4 Dimensions.  My ability to draw diagrams in 4-D is very limited, so we will not have any this time.

We need to pick a point in 4 dimensions that does not exist anywhere in our 3-D world.  At the start, we might be tempted to think that such a world is simply unphysical and impossible until we consider that the 4th dimension might be related to time.  Consider a point (x, y, z, t), where ‘t’ represents the time (watch) that is associated with the point (x, y, z).  Does this even make sense, points running around with timer watches?

     It might be easier to believe if we consider a single point that is able to move around in 3-D space.  When we track the same point (x, y, z) over time, we can imagine that it doesn’t have to be in the same position all the time relative to where it is right now.  If we want to track the movement of a point through time, then its associated timer watch (t) comes in handy.  We can think of the path of the point walking through time as walking through a path in 4-D “space-time”, where the point (x, y, z, t) describes the position of the point (x, y, z) at the time ‘t’.

Suppose that we choose the origin (0, 0, 0, 0) to be the position of the point when we set the timer to zero.  Then a “new point” in 4-D space-time could be (0, 0, 0, 1) which describes the same point in the same place 1 second later. We are getting closer to constructing our new 4-D space.  Now we need to draw line segments from every point in 3-D space to this new point in 4-D space-time and then need to locate the shortest of these line segments (like we did when expanding 2 dimensions to 3 dimensions).

A problem arises, however, because the time ‘t’ is not a distance, so it is confusing to find a measure for distance in this 4-D space.  What is x2 + y2 + z2 + t2?  One way to solve this problem is to somehow convert the time ‘t’ into a measure of distance:

    (Distance/Time)*Time = Distance

By choosing a constant speed ‘C’  (with units of Distance/Time) that is the same for every point in this 4-D space, we have a way to convert any time into a distance:

      C*t = the distance traveled in time ‘t’

So, if C is truly a constant speed for all points in space-time, then ‘C*t’ is the distance that any point with this constant speed ‘C’ would travel in a time ‘t’.  So let us redefine a point in 4-D space time to be described by:

   (x, y, z, C*t)

And we have a 4-D space of distances.  Then distance ‘S’ between the origin (0, 0, 0, 0) and any point (x, y, z, C*t) is found to be:

   S2 = x2 + y2 + z2 + (C*t)2

And, as usual, the direction ‘D’ of a line from the origin to any point can be expressed as the vector:

    D = (Dx, Dy, Dz, Dt)

      where

    D.D = Dx2 + Dy2 + Dz2 + Dt2 = 1

Here Dt expresses how fast time is changing as you travel a 4-D distance ‘S’ along the line.  As usual, lines from the origin in 4-D spacetime can be expressed as:

     (x, y, z, C*t) = (Dx, Dy, Dz, Dt)*S

                        or

     (x, y, z, C*t) = (Dx*S, Dy*S, Dz*S, Dt*S)

‘Dx*S’ expresses how far the point has traveled in the x-direction, as usual, and the other 3-D coordinates have similar meanings.  The new one is ‘Dt*S’ that describes how much time has elapsed after we have traveled a distance ‘S’ along this 4-D line.  Dt determines the speed of the timer.  Notice that the 4-D distance ‘S’ is not the same as the 3-D distance we will now call ‘S3’:

     S32 = (Dx*S)2 + (Dy*S)2 + (Dz*S)2
         = (Dx2 + Dy2 + Dz2)*S2

Since 1 – Dt2 = Dx2 + Dy2 + Dz2, we see a more interesting expression for S3:

   S32 = (1 – Dt2)*S2

This is interesting, and maybe a bit surprising, because it says that the distance that the point (x, y, z, C*t) travels in 3-D space is completely determined by the Dt direction parameter of the 4-D line.  If you look at it a bit closer, however, it starts to make sense.  Since 1 – Dt2 = Dx2 + Dy2 + Dz2 then when Dt = 1, the other direction parameters, Dx2, Dy2, and Dz2 must add to zero.  Thus (Dx, Dy, Dz, Dt) must be (0, 0, 0, 1), and the point is only moving in the ‘time’ direction, but not moving in any of the 3-D directions.  This 4-D direction describes a point that is not moving in 3-D space, S32 = 0.

If Dt is less than 1 then the point has room to move in 3-D space.  A more perplexing situation happens when Dt = 0.  Then in this direction, time stands still, no time is elapsing, but the point can go any distance it wants in the 3-D space.  Physically this makes very little sense.  The point could be everywhere all at once. Let’s look at what this means in terms of the speed ‘V’ of the point.  Speed is the 3-D distance it travels per the time elapsed ‘t’ (recall C*t = Dt*S):

    V = S3/t
    V = C*S3/(Dt*S)

    V2 = C2*S32/(Dt*S)2
         = C2*(1 – Dt2)*S2/(Dt2*S2)
         = C2*(1 – Dt2)/Dt2

And we see that the speed of the point is constant everywhere on the 4-D line and it is completely determined by how fast the point is traveling in the ‘time’ direction, Dt.  Things also start to be more understandable.  However, if Dt goes to zero, then the speed is infinitely fast (you can’t divide by zero).  Having things that can go at infinite speed is very problematic.  The point could literally be everywhere at once.  One fun definition of time is: “Time is something that keeps everything from happening all at once”.  It makes sense to have some sort of a speed limit for our points.

Einstein, a brilliant physicist, made the argument that the speed ‘C’ (a constant speed for all points in space-time) should be that speed limit.  If we assume this (C2 >= V2), then we can find restrictions on the direction parameter Dt:

     C2 >= C2*(1 – Dt2)/Dt2
      1 >= (1 – Dt2)/Dt2
      Dt2 >= ½

This puts some serious restrictions on the directions of lines that are possible to traverse in space-time:

    ½ <= Dt2 <= 1

Dt is between the square root of ½ and 1.  Another restriction that we see is that we cannot go backwards in time, Dt cannot cross over to become negative unless the point violates the speed limit and can go infinitely fast.

So, a 4-D space-time can exist mathematically, but for it to make sense physically, certain restrictions must be placed on the directions of lines we can draw in this space-time. Next time, we will look at how to find (Dx, Dy, Dz, Dt) in space-time and their associated angles.  We will introduce a new angle, At, that describes the angle of the “time” direction.  We will find that Dt = Sin(At).  At the speed limit ‘C’, Dt is the square root of ½.  From trig this means that At = 45 degrees.  The restrictions require that At is between 45 degrees and 90 degrees.  This “cone” of 4-D space-time is the only place where anything can exist when it comes from the origin.  It is commonly called the “light cone”. And the speed of light is the speed limit ‘C’.

Standard

Math Moments – Navigating in 3-D Space

We can navigate in 3-D to any point (xR, yR, zR), in Cartesian Coordinates, by starting at the origin (0, 0, 0) and in the 2-D, x-y plane, walking in the x-direction (1, 0, 0) a distance xR, then turning left 90 degrees and walking a distance yR in the y-direction (0, 1, 0), still on the x-y plane.  This is the same as we did in 2-D except we put an extra ‘0’ in the third ‘z’ direction.  At this point we are still on the x-y plane at the point (xR, yR, 0).  The z-direction is straight up, so we would now need a ladder to climb up or a shovel to dig down, it is helpful to pretend we can fly (or dig).  From this point (xR, yR, 0) on the x-y “ground” plane, we fly straight up in the z-direction (0, 0, 1) a distance zR, and we successfully arrive at the point (xR, yR, zR).

We can express this journey with vectors, as we did in 2-D, by connecting (adding) lines together to form the path:

   (xR, yR, zR) = (1, 0, 0)*xR + (0, 1, 0)*yR + (0, 0, 1)*zR
                        = (xR, 0, 0) + (0, yR, 0) + (0, 0, zR)
                        = (xR, yR, zR)

        And using dot product notation, this can be written:

   (xR, yR, zR) = (1, 0, 0)*xR + (0, 1, 0)*yR + (0, 0, 1)*zR
                        = [(1, 0, 0), (0, 1, 0), (0, 0, 1)].(xR, yR, zR)

The [(1, 0, 0), (0, 1, 0), (0, 0, 1)] matrix is called the identity matrix.

We could also arrive faster by flying along a straight line connecting the two. Fly along a direction (Dx, Dy, Dz), from the origin directly to this point, (xR, yR, zR) a distance “R” away:

   (xR, yR, zR) = (Dx, Dy, Dz)*R

        Where the distance ‘R’ is found by:

    R2 = xR2 + yR2 + zR2

From the equation above for this line, we can easily find the direction vector from the origin to any point (xR, yR, zR), similar to what we did in 2-D.

      (Dx, Dy, Dz) = (xR/R, yR/R, zR/R)

Recall that the direction vector always has a distance of 1 unit, as seen in the diagram above.  In the diagram, we have attempted to show a 3-D path on a 2-D piece of paper.  Note that in the diagram, Dr is the distance from the origin to the point (Dx, Dy, 0) in the x-y plane. From the Pythagorean theorem, we find that the length:

      Dr2 = Dx2 + Dy2    and
      Dr2 + Dz2 = 1        thus combining these
      Dx2 + Dy2 + Dz2 = 1.

The total length of the distance vector is 1 unit, as required.  Everything is consistent.  Now we use the definition of the ‘Sin’ and ‘Cos’ and can see, from the diagram above, that:

     Cos(Axy) = Dx/Dr
     Sin(Axy) = Dy/Dr

      Cos(Az) = Dr/1
      Sin(Az) = Dz/1

    Thus

       Dx = Cos(Axy)*Dr = Cos(Axy)*Cos(Az)
       Dy = Sin(Axy)*Dr = Sin(Axy)*Cos(Az)
       Dz = Sin(Az)

And so, if we stand at the origin facing in the x-direction, and rotate our “head” an angle Axy to the left, and then tilt our head an angle Az off the x-y plane to look directly at the point (xR, yR, zR), we can find the direction vector pointing to this point using these angles:

   (Dx, Dy, Dz) = (Cos(Axy)*Cos(Az), Sin(Axy)*Cos(Az), Sin(Az))

       And then draw the line to this point:

    (xR, yR, zR) = (Dx, Dy, Dz)*R

Now that we are staring at a point in the sky, with our nose pointed directly at the point, we can ask about “reference frame” of our head.  What direction is our left ear pointing, for example.  Our left ear is pointing in the direction, still in the x-y plane, that is 90 to the left of the Axy angle we rotated our head (-Dy/Dr, Dx/Dr, 0). We divide by Dr because in 3-D we must make the length of the direction vector equal to 1.  If this seems vague, look back and review how to find 90 degree directions in the 2-D plane in the top diagram taken from previous posts.

When we tilt our head, we can ask what is the direction that the top of our head points, 90 degrees up from the angle Az. It perhaps takes a bit more imagination to see this, since we are facing in the x-y plane (Dx/Dr, Dy/Dr, 0) and have tilted our head up to look at Dz, we find that the “shadow” of our head is pointed behind us, in the x-y plane (-Dx/Dr, -Dy/Dr, 0), then looking at the elevation Dr (when rotated 90 degrees) we find that (-Dx*Dz/Dr, -Dy*Dz/Dr, Dr) is the direction of the top of our head.  So, in the reference frame of our head:

     Direction of our Nose:     (Dx, Dy, Dz)
     Direction of Left ear:         (-Dy/Dr, Dx/Dr, 0)
     Direction of Top of head:  (-Dx*Dz/Dr, -Dy*Dz/Dr, Dr)

Let us verify that these direction vectors all have a length of 1.  The Nose direction we have verified.  For the Left ear direction:

    L.L = (-Dy/Dr)2 + (Dx/Dr)2 + 02 = (Dy2 + Dx2)/Dr2 = 1

For the Top of head direction:

    T.T = (-Dx*Dz/Dr)2 + (-Dy*Dz/Dr)2 + Dr2 = (Dy2 + Dx2)*Dz2/Dr2 + Dr2
                                                                    = Dz2 + Dr2 = 1

Now let’s find what happens when we find the dot product of these direction vectors, we will call them the N, L, and T directions respectively.

N.N = (Dx, Dy, Dz).(Dx, Dy, Dz) = Dx2 + Dy2 + Dz2 = 1

N.L = (Dx, Dy, Dz).(-Dy/Dr, Dx/Dr, 0) = -Dx*Dy/Dr + Dy*Dx/Dr + 0
                                                                  = 0

N.T = (Dx, Dy, Dz).(-Dx*Dz/Dr, -Dy*Dz/Dr, Dr)
        = -Dx2*Dz/Dr + -Dy2*Dz/Dr + Dz*Dr
        = -(Dx2 + Dy2)*Dz/Dr + Dz*Dr
        = -Dr2*Dz/Dr + Dz*Dr
        = 0

L.T = (-Dy/Dr, Dx/Dr, 0).( -Dx*Dz/Dr, -Dy*Dz/Dr, Dr)
       = Dy*Dx*Dz/Dr2 + -Dx*Dy*Dz/Dr2 + 0
       = 0

We also verified that L.L = 1 and T.T = 1 above.  So, in general, if we dot any of these N, L, T direction vectors with themselves, we get ‘1’, but if we dot any of them with each other, we get ‘0’.  It turns out that this is a requirement for any three perpendicular direction vectors in a 3-D Cartesian reference frame.  I find the “head” reference frame to be more natural because we can relate to it better, so I use this reference frame for whatever direction I am looking.  It is also a great reference frame for video games.

We have already seen from perpendicular 2-D paths how we can convert between a reference frame to our “ground” x-y-z reference frame.  To understand this, let’s take a journey: Fly in the Nose direction a distance SN, then fly in the Left ear direction a distance SL, and then in the Top of head direction a distance ST.  Then we will arrive at the point:

    (x, y, z) = N*SN + L*SL + T*ST

       or in dot product notation:

     (x, y, z) = [N, L, T].(SN, SL, ST)

This amazing equation lets you convert any point in your “head frame” of reference (SN, SL, ST), when your Nose is pointing in a direction N:(Dx, Dy, Dz), to a point in the “ground” frame (x, y, z).  You might also want to do this the other way around.  Review how we did this in 2-D, by “dotting” each side by each of the direction vectors, we get:

    (SN, SL, ST) = [N, L, T].(x, y, z)

This is how video games convert a 3-D world, stored in “ground” (x, y, z) coordinates, into the perspective of the viewer’s head (SN, SL, ST) coordinates.  The details need to be worked out but using this equation we can map a 3-D world onto a 2-D screen in the viewer’s perspective, no matter the relative direction of the viewer’s head.  We will stop here, there is a lot to take in.

Standard

Math Moments – The Rotation Matrix

On the Cartesian plane, if we walk along the x-direction (1, 0) for a distance of 4 units, then turn left 90 degrees (perpendicular) and walk a distance of 3 units, we arrive at the point (4, 3), which is a distance of 5 units from the origin (42 + 32 = 52), great.  Well, what happens if we do the same, but start off walking in any direction (Dx, Dy) 4 units and then turn left 90 degrees (-Dy, Dx) and walk 3 units; we are still 5 units from the origin.  We have just “rotated” the whole path to a new direction.  Where would we end up (x, y)?  We use our orienteering skills:

     (x, y) = (Dx, Dy)*4 + (-Dy, Dx)*3
     (x, y) = [(Dx, Dy), (-Dy, Dx)].(4, 3)  –  using the dot product

Now notice that the matrix [(Dx, Dy), (-Dy, Dx)] when dotted with the cartesian point (4, 3) rotates it to another point on the circle (radius 5).  See the diagram. This matrix is called the “rotation matrix”.

Now that we are getting a bit more comfortable with the dot product, let’s play around and see what happens when we dot direction vectors with each other?  We’ll start off by dotting a direction with itself:

     (Dx, Dy).(Dx, Dy) = Dx2 + Dy2 = 1

Any direction dotted with itself is just “1”.  What about dotting a direction with its perpendicular direction?

    (Dx, Dy).(-Dy, Dx) = Dx*(-Dy) + Dy*Dx = 0

It turns out that any direction dotted with its perpendicular direction is “0”.  Now how about dotting the position (x, y) above with the direction vector?

   (Dx, Dy).(x, y) = (Dx, Dy).((Dx, Dy)*4 + (-Dy, Dx)*3)
                             = (Dx, Dy).(Dx, Dy)*4 + (Dx, Dy).(-Dy, Dx)*3
                             = 1*4 + 0*3
                             = 4

And so, dotting a direction vector (Dx, Dy) with any position vector (x, y) gives you the distance (Sx) you would have to travel in that direction before making a 90 turn and traveling the distance (Sy) that would bring you to the position (x, y).  Now let’s dot the perpendicular direction with the position vector:

   (-Dy, Dx).(x, y) = (-Dy, Dx).((Dx, Dy)*4 + (-Dy, Dx)*3)
                             = (-Dy, Dx).(Dx, Dy)*4 + (-Dy, Dx).(-Dy, Dx)*3
                             = 0*4 + 1*3
                             = 3

You can see that dotting the perpendicular direction with a position also gives you the distance (Sy) you would have to travel in the perpendicular direction (-Dy, Dx) to get to the position (x, y).

And so can you see that in this case:

     [(Dx, Dy), (-Dy, Dx)].(x, y) = (4, 3)

So in general if

     (x, y) = [(Dx, Dy), (-Dy, Dx)].(Sx, Sy)

              then

     [(Dx, Dy), (-Dy, Dx)].(x, y) = (Sx, Sy)

What does this mean?  The rotation matrix […] when it “operates” on (is dotted with) any point (x, y), gives you the coordinates of the point relative to a new set of “x-y” axis that is pointing in a direction (Dx, Dy) relative to the old axis.  Or you can say that it rotates the point around the origin.  Either vantage point is valid, you can rotate the point around the origin or rotate the reference frame in the opposite way around the origin; either way, it is describing the same thing.

Remember the concept of “rotational symmetry”, that we can pick the direction of the x-y axis to be in any direction we want.  Now we have the tools to convert the cartesian coordinates of a set of points from any reference frame to a reference frame pointing in any direction we choose.

THIS IS A FUNDAMENTAL CONCEPT of the MATH Language: ROTATIONAL SYMMETRY means that the universe is the same no matter the direction of your frame of reference.  The Rotation matrix gives you a way of describing the same universe from any prospective of direction.  It is pure magic.

One more point, remember that

   (Dx, Dy) = (Cos(A), Sin(A))

Where “A” is the angle of the direction off x-axis.  Thus, the rotation matrix “R(A)” can be written as:

     R(A) = [(Cos(A), Sin(A)), (-Sin(A), Cos(A))]

And there you have it.

Standard

Math Moments – Constructing Parallel Universes

The diagram above (which looks a little like Homer Simpson) shows you how to build a 2-dimensional universe from 1-dimensional universes. There is a lot in the diagram so we will go over it a piece at a time then you can use your imagination to build another universe.

Start with the original 1-dimensional line, the one that passes through the points labeled O, and O+ on the diagram. Remember that we need only 2 points on the line, any 2 of them will generate the whole line. We then need to find another point, labeled P, that is not on the original line. The lines radiating out of the point P represent all the lines connecting P with all the points on the original line “O”.

Each one of the line segments between point P with a point on the line spans a different distance. We find a line of symmetry with respect to P by finding the segment with the shortest distance. This segment goes to the point labeled O. Point O is an important point of reflection, a point of symmetry on the line with respect to P, any point on the positive side of O and its reflection on the negative side of O has the same distance to Point P.

We use the label “r” to refer to the distance between point P and point O. In math language, the symbol “r” reminds us of a “radial” distance from the point P. This r distance is referred to as the “distance” between P and the line. If we put together all the points (on the radial lines) that are a distance r from point P, we form a circle of radius r around P. Notice that since r is the shortest distance between P and the line, this circle only touches the line at point O and cannot reach the line anywhere else. Can you find this circle in the diagram?

The line passing through O and P is a special line of symmetry in this case. It is often called the “normal” of the line that passes through point P. It is also called the perpendicular to the line passing through P. Any set of points on the “positive” side of a line can be reflected onto the “negative” side by finding the perpendiculars passing through the points and then reflecting the points along their perpendicular lines the same distance on the “negative” side of the line. In this diagram, this symmetry is obvious, every point on the right (+) side of the perpendicular (O P) is a reflection of points the left (-) side and vice versa.

In the diagram, we show the point O+ on the positive side of the original line at a distance r from the point O. Its reflection on the negative side is labeled O-. We can easily see that the line (O O+) is also the perpendicular of the line (O P). If we wanted to, we could reflect this whole diagram through the original line and we would get the diagram flipped upside down on the bottom half. For clarity’s sake, I didn’t do this in the diagram.

You might be starting to see the amazing symmetries represented in this diagram. It gets even more obvious when you look at the midpoint between O+ and P. This is labeled M+. Its reflection is labeled M-. If we draw a line segment between M+ and M-, as shown in the diagram, notice that it is also perpendicular to the line of symmetry. To show this better I drew a circle around point M+ and M- that touches the perpendicular line at one point. It also becomes obvious that M+ and M- are the same distance from the original line O O+, by symmetry. All distances are preserved upon reflection.

Alright, now we use our imagination to see what would happen if we drew another perpendicular to the original line through point M+ and another through M-. We can use the small circles drawn to visualize where the circle touches the line to draw these perpendiculars. We can now reflect everything in the middle of these perpendiculars on either side. Like two mirrors facing each other, the reflections go on forever in both directions.
From these symmetries, the line M- M+ can be shown to always be the same distance away from the original line forever in both directions. These lines will never cross.

We have finally found two parallel 1-dimensional spaces that do not intersect each other. Do you think you could find an infinite number of parallel lines in the vertical direction by using reflections?

This is a concept utilized by the mathematician Rene Descartes. He built what is known as the Cartesian plane, composed of infinitesimally close parallel vertical and horizontal lines all normal to each other. These concepts give us many ways to look at 2-dimensional space. One of the most important qualities of this space is that it is assumed to be exactly the same in all directions. Very flat indeed.

Standard

Math Moments – Expanding into Parallel Universes

Alright, this is where it starts getting really interesting. We started out saying that we can use the language of math to build universes, at least in our imagination. We started out with (1) one point in the whole universe. Since a point has no size, the whole universe was simply a 0-dimensional space (a bit mind blowing).

After thinking about nothing for a while, we then thought about having (2) two points in the universe. We argued the concept of distance between these two points. We imagined two distinct completely identical points separated by a distance, this is the origin of the concept of the number 2. We then discussed a way to build a whole 1-dimensional space of points, a line between the two points.

We said that we could fill in the points on a line between these two points by first creating a midpoint a distance half-way between these points then, including the midpoint, use the same concept to create more new points in the middle of these points, and so on forever filling in the gaps (a bit more mind blowing).

We realized that there are an infinite number of points that can fit between our original 2 points, each of them described by the distance and direction they are from the midpoint. We started finding other points to fill in all the gaps between points.

We introduced the concept of symmetry; for every point on the line, everything must look exactly the same in both directions. This symmetry concept required that every point on the line has the same arrangement of points in either direction. If we ever found a point where the line ends, we could just add another segment onto the empty direction and keep doing this forever. This complete infinite 1-dimensional space of points is called a “line” (oh, the things we can think).

We named the two directions in this 1-dimensional space to be “negative” and “positive”. We can now choose any of the points to be a reference point and describe the position of any point in this space by its distance and direction from the reference point. We have thus introduced the number line.

I hope you enjoyed this line of reasoning so far. We can now use the same line of reasoning we used to expand 0-dimensional space into 1-dimensional space in order to expand a 1-dimensional space into a 2-dimensional space.
As before, we only need to take the points we have in a 1-D space, on the line, and introduce another new point that is not in that space, not on the line. With this new point, we can now define another line by using this new point and any of the points on the original line to create a new line going in a different direction.

Since we can now create a distinct new line through the new point for every point on the original line, we have created an infinite array of new lines (1-D spaces) going off in different directions. Since the points on the original line can be infinitesimally close together, so are the lines. We include all the points on all these lines as part of a new 2-D space. We now have lots of points to connect together to form new lines. All these lines are said to live in this new 2-D space. An ancient mathematician, Euclid, studied these spaces, in honor of him, these “flat” spaces, of straight and parallel lines are called Euclidean spaces.

There are still some gaps. For example, there is a line that passes through the new point that is not connected to the original line, this line is said to be “parallel” to the original line, and since it never can cross the original line, it does not contain any of the points of the original line. As it turns out, building parallel lines using the tools we have requires a bit of doing.

Standard

Math Moments – Extending Spaces into New Dimensions

So far, we have been exploring a 1-dimensional “space” of points along an infinitesimally thin line. Mathematicians call this a 1-dimentional space. The concept of symmetry implies that the line looks exactly the same in both directions. Therefore, this line must extend on forever in both directions, there is no point on the line where it ends. The line looks exactly the same on both sides of every point.

The concept of point symmetry in 1-dimensional space also means that if you were to reverse the direction of the “ruler” that measures the distance between any two points in this space, you will still measure the same distance between the points. This concept of invariance of direction is one of the most important characteristics of space. Of course, we need a lot more than just one line to describe all the space around us.

In order to expand the dimensions of space beyond this 1-dimensional space, we must assume that there is some point that is not in this space, a point that is not on the line. When we find a point that is not on the line, we can create a new line between any point on the line and the new point. This defines a new 1-dimensional space (a line) for every point on the original line, all of these new lines pass through the new point.

Since there are an infinite number of points on the original line, we see that there are an infinite number of 1-dimensional lines that can be drawn through the new point all in different directions. The space formed by this infinite number of lines is called a 2-dimensional space. It is called 2-dimensional due to the “language” necessary to describe the location of any point in this space. To locate any point, we must choose a reference point, then first (1) we need to choose one of the lines passing through the reference point, and second (2) we use the methods we have already discussed to determine the location of a point along this reference line. Thus, the location of a point thus requires 2 numbers, one (1) to locate the reference line, and the other (2) to determine the location of the point along this line.

The concept of point symmetry in 2-dimensional spaces also comes into play. It means that measuring distances is the same in every direction. This invariance of direction means that if we have a “ruler” that measures a distance along any of the lines in this space, and we change the direction of the ruler, the length of the ruler does not change.

Imagine how the world would look if measuring lengths in one direction were different than lengths in another direction. If the invariance of direction was not true, then when we changed direction, the distance between things would shorten or lengthen, depending on which direction we faced. This is not what we experience in real life.

We can use the same concepts that we used to extend 1-dimensional space to 2-dimensional space to extend into spaces into any number of dimensions. How many distinct points do you need to generate a 3-dimensional space? Think about it. We will discuss how it can be done later.

Standard

Math Moments – The power of symmetry

If we were to consider any two points in the universe (A and C) and draw an imaginary line segment between these two points, there would be only one singular point on that line segment that preserves symmetry (under reflection). This is the midpoint (B) on the line segment which is exactly the same distance from each of the endpoints. You can reflect (flip) either one of the endpoints through the midpoint and it would fall exactly on the other endpoint. Such symmetry applies to all points on the line segment that are the same distance from this midpoint.

If you were to pick the midpoint as the reference point and the positive direction pointing toward one of the endpoints, then from the midpoint, the line segment in the positive direction looks exactly the same as the line segment in the negative direction. You could conceptually switch the positive direction with the negative direction, and nothing would change. This is called reflection symmetry, for obvious reasons.

If you have reflection symmetry, then anything that exists at a certain distance along the positive direction, also exists at that same distance in the negative direction; just like looking at things through a mirror. We use such symmetries in atomic physics all the time to make things easier.

For example, the electric field between two identical electrons, as observed from the midpoint between them, looks exactly the same when you are facing one electron as it does when you are facing the other. From the midpoint, everything is exactly the same in both directions, you cannot tell the difference between the electrons nor any of their physical properties from this perspective. To tell the difference, you would need to “break the symmetry” by introducing something else that is not symmetric to the midpoint.

So, once you have seen what exists on one side of the “mirror” we also know what will exist on the other side. It makes the math (and the diagrams) so much easier. We always should seek out these points of symmetry when we are doing the math, it makes everything so much more…symmetric.

Standard