Tag Archives: physics

Math Moments – A New Perspective

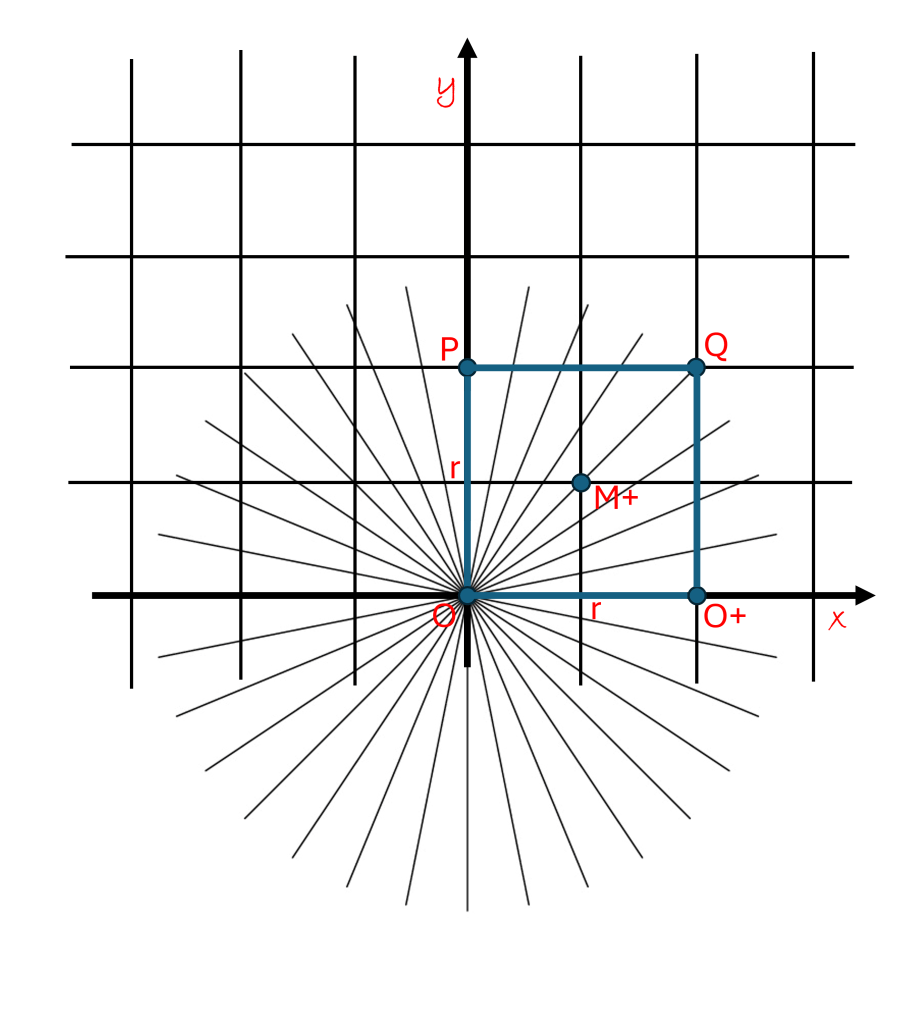
You can learn a lot about something when looking at it from a new perspective. In the diagram above we are looking at the exact same square as in the last post from a different vantage point. Again, I use my right to choose a reference point and direction. I keep the point O as my reference point, but I rotate the cartesian grid a bit clockwise.

Notice that I have not changed anything about the square, it has the same points. I have only changed the way I am looking at the square. The area of the square has not changed, it is still r2. I have just “tilted my head” a little bit. I chose an “x” direction that is not along the O O+ side of the square and the “y” direction to be perpendicular. This is certainly within my rights under the axiom of choice.

From this perspective, however, the way I measure the area of the square is a bit different, I cannot “tile” the square with the cartesian tiles in this direction without “cutting off” the corners of the tiles. From here grows the whole field of trigonometry. I need to rotate my ruler to measure distance from any point and in any direction in 2-D space.

In the diagram above, I am looking at the “bottom” line segment of the square, O O+, from this new perspective, I have also modified the grid spacing a bit for better clarity. In this diagram, I found the “coordinates” of the O+ point by finding the perpendicular distance from both the x and y axis, as is customary. The distance away from the y axis is labeled “x”, and the distance away from the x axis is labeled “y”.

It is obvious from the diagram that, by parallel sides, the respective distances from O+ form a rectangle with one side a distance “x” along the x axis and another side a distance “y” along the y axis. These distances are called the cartesian “coordinates” of the point O+. It is also obvious that the area of this rectangle is x times y, written as x*y ( we use “*” to mean “multiplied by” for clarity).

If I now choose the O+ point to be the point of reference and chose the “y” direction to be down and “x” direction to be to the left, as shown by the yellow script “x” and “y” in the diagram, I basically would have chosen to look at this same rectangle from an “upside down” perspective. By flipping the diagram upside down, you can see that the rectangle and O O+ line segment looks exactly the same from this perspective.

This shows an important symmetry of the rectangle. It also shows that the area of the triangle on the top half of the rectangle is exactly the same as the area of the triangle on the bottom half. Or to say, the segment O O+ cuts the rectangle in half. Thus, the area of both triangles is ½ * x * y. This also shows that the angles of both corresponding triangles are exactly the same. We will talk about this later.

The equivalence of areas (the real estate of 2-D), regardless of our choice of reference point and direction, gives us a way to “rotate” our ruler into any angle and direction. This relation was found by Pythagoras many millennia ago and is called the Pythagorean theorem.

Standard

Math Moments – 2-Dimensional Real Estate

In the last post’s “cartesian grid” diagram, if you remember, the radial lines went through the point P. By reflection symmetry, I can reflect these radial lines onto any cartesian grid point I want. In the diagram above, I decided to reflect the radial lines so they now radiate from point O. I now choose point O to be the reference point.

I choose one of the “cartesian” directions to be from the reference point O to the point O+, I will call this direction the positive “x” direction, labeled by the red script “x”. I call this line the “x” axis, shown as a bold horizontal line in the diagram.

The second “cartesian” direction I choose to be from the reference point O to the point P. I call this direction the positive “y” direction (as customary), and label it with a red script “y”. This vertical line in the diagram is called the “y” axis and is bolded. There are always two perpendicular independent directions I can choose in a 2-D space. The axiom of choice allows me to choose whatever reference point I want and whatever two reference directions I want. As mentioned before, the right to choose is one of the fundamental concepts of math.

Alright, let’s talk money. In 1-D space, distance is everything, it is the most valuable asset, but in 2-D, distance alone is not worth anything. A piece of land that is 10 meters long has no value until you know how wide it is. The real estate of 2-dimensional space is called “area”. Area is measured by how many squares, or fractions of squares can fit within a given border. The number of squares determines the value.

In the diagram, we form a square by taking the segment O O+ (of length r) and the perpendicular segment O P (also of length r) and reflecting them through M+ to form the opposite sides P Q and O+ Q. Note that we found a point Q that is exactly the distance “r” from both the “x” and the “y” axis. This square (in green) now has value, it is the real estate of 2-D space.

We have seen that the whole 2-dimensional space can be “tiled” with the squares of a cartesian grid. The number of “tiles” within a boundary determines the area. For example, in the diagram above, the green r x r square has 4 cartesian tiles inside. Each side has 2 tiles and 2 x 2 = 4 tiles. Since we could shrink the size of the tiles, we could also fill the square with lots of tiny tiles. From this, it can be deducted that the area of the square is found by multiplying the length of the square by the width of the square (r x r = r2).

The area of the green square in the diagram is r2. In 2-dimensions, the “real estate” or area is always measured as a distance times a distance, like a square meter, or a square foot. In 2-D, a line segment alone has no width, and so it has no area, and thus line segments have no real value in 2-D space.

In concept, you can fit an infinite amount of parallel line segments into a square no matter how small it is. This becomes clear when we recall the same concept in 1-D space to show that an infinite number of points can fit between any two points on a line segment, no matter how small.

Standard

Math Moments – Constructing Parallel Universes

The diagram above (which looks a little like Homer Simpson) shows you how to build a 2-dimensional universe from 1-dimensional universes. There is a lot in the diagram so we will go over it a piece at a time then you can use your imagination to build another universe.

Start with the original 1-dimensional line, the one that passes through the points labeled O, and O+ on the diagram. Remember that we need only 2 points on the line, any 2 of them will generate the whole line. We then need to find another point, labeled P, that is not on the original line. The lines radiating out of the point P represent all the lines connecting P with all the points on the original line “O”.

Each one of the line segments between point P with a point on the line spans a different distance. We find a line of symmetry with respect to P by finding the segment with the shortest distance. This segment goes to the point labeled O. Point O is an important point of reflection, a point of symmetry on the line with respect to P, any point on the positive side of O and its reflection on the negative side of O has the same distance to Point P.

We use the label “r” to refer to the distance between point P and point O. In math language, the symbol “r” reminds us of a “radial” distance from the point P. This r distance is referred to as the “distance” between P and the line. If we put together all the points (on the radial lines) that are a distance r from point P, we form a circle of radius r around P. Notice that since r is the shortest distance between P and the line, this circle only touches the line at point O and cannot reach the line anywhere else. Can you find this circle in the diagram?

The line passing through O and P is a special line of symmetry in this case. It is often called the “normal” of the line that passes through point P. It is also called the perpendicular to the line passing through P. Any set of points on the “positive” side of a line can be reflected onto the “negative” side by finding the perpendiculars passing through the points and then reflecting the points along their perpendicular lines the same distance on the “negative” side of the line. In this diagram, this symmetry is obvious, every point on the right (+) side of the perpendicular (O P) is a reflection of points the left (-) side and vice versa.

In the diagram, we show the point O+ on the positive side of the original line at a distance r from the point O. Its reflection on the negative side is labeled O-. We can easily see that the line (O O+) is also the perpendicular of the line (O P). If we wanted to, we could reflect this whole diagram through the original line and we would get the diagram flipped upside down on the bottom half. For clarity’s sake, I didn’t do this in the diagram.

You might be starting to see the amazing symmetries represented in this diagram. It gets even more obvious when you look at the midpoint between O+ and P. This is labeled M+. Its reflection is labeled M-. If we draw a line segment between M+ and M-, as shown in the diagram, notice that it is also perpendicular to the line of symmetry. To show this better I drew a circle around point M+ and M- that touches the perpendicular line at one point. It also becomes obvious that M+ and M- are the same distance from the original line O O+, by symmetry. All distances are preserved upon reflection.

Alright, now we use our imagination to see what would happen if we drew another perpendicular to the original line through point M+ and another through M-. We can use the small circles drawn to visualize where the circle touches the line to draw these perpendiculars. We can now reflect everything in the middle of these perpendiculars on either side. Like two mirrors facing each other, the reflections go on forever in both directions.
From these symmetries, the line M- M+ can be shown to always be the same distance away from the original line forever in both directions. These lines will never cross.

We have finally found two parallel 1-dimensional spaces that do not intersect each other. Do you think you could find an infinite number of parallel lines in the vertical direction by using reflections?

This is a concept utilized by the mathematician Rene Descartes. He built what is known as the Cartesian plane, composed of infinitesimally close parallel vertical and horizontal lines all normal to each other. These concepts give us many ways to look at 2-dimensional space. One of the most important qualities of this space is that it is assumed to be exactly the same in all directions. Very flat indeed.

Standard

Math Moments – Expanding into Parallel Universes

Alright, this is where it starts getting really interesting. We started out saying that we can use the language of math to build universes, at least in our imagination. We started out with (1) one point in the whole universe. Since a point has no size, the whole universe was simply a 0-dimensional space (a bit mind blowing).

After thinking about nothing for a while, we then thought about having (2) two points in the universe. We argued the concept of distance between these two points. We imagined two distinct completely identical points separated by a distance, this is the origin of the concept of the number 2. We then discussed a way to build a whole 1-dimensional space of points, a line between the two points.

We said that we could fill in the points on a line between these two points by first creating a midpoint a distance half-way between these points then, including the midpoint, use the same concept to create more new points in the middle of these points, and so on forever filling in the gaps (a bit more mind blowing).

We realized that there are an infinite number of points that can fit between our original 2 points, each of them described by the distance and direction they are from the midpoint. We started finding other points to fill in all the gaps between points.

We introduced the concept of symmetry; for every point on the line, everything must look exactly the same in both directions. This symmetry concept required that every point on the line has the same arrangement of points in either direction. If we ever found a point where the line ends, we could just add another segment onto the empty direction and keep doing this forever. This complete infinite 1-dimensional space of points is called a “line” (oh, the things we can think).

We named the two directions in this 1-dimensional space to be “negative” and “positive”. We can now choose any of the points to be a reference point and describe the position of any point in this space by its distance and direction from the reference point. We have thus introduced the number line.

I hope you enjoyed this line of reasoning so far. We can now use the same line of reasoning we used to expand 0-dimensional space into 1-dimensional space in order to expand a 1-dimensional space into a 2-dimensional space.
As before, we only need to take the points we have in a 1-D space, on the line, and introduce another new point that is not in that space, not on the line. With this new point, we can now define another line by using this new point and any of the points on the original line to create a new line going in a different direction.

Since we can now create a distinct new line through the new point for every point on the original line, we have created an infinite array of new lines (1-D spaces) going off in different directions. Since the points on the original line can be infinitesimally close together, so are the lines. We include all the points on all these lines as part of a new 2-D space. We now have lots of points to connect together to form new lines. All these lines are said to live in this new 2-D space. An ancient mathematician, Euclid, studied these spaces, in honor of him, these “flat” spaces, of straight and parallel lines are called Euclidean spaces.

There are still some gaps. For example, there is a line that passes through the new point that is not connected to the original line, this line is said to be “parallel” to the original line, and since it never can cross the original line, it does not contain any of the points of the original line. As it turns out, building parallel lines using the tools we have requires a bit of doing.

Standard

Math Moments – Extending Spaces into New Dimensions

So far, we have been exploring a 1-dimensional “space” of points along an infinitesimally thin line. Mathematicians call this a 1-dimentional space. The concept of symmetry implies that the line looks exactly the same in both directions. Therefore, this line must extend on forever in both directions, there is no point on the line where it ends. The line looks exactly the same on both sides of every point.

The concept of point symmetry in 1-dimensional space also means that if you were to reverse the direction of the “ruler” that measures the distance between any two points in this space, you will still measure the same distance between the points. This concept of invariance of direction is one of the most important characteristics of space. Of course, we need a lot more than just one line to describe all the space around us.

In order to expand the dimensions of space beyond this 1-dimensional space, we must assume that there is some point that is not in this space, a point that is not on the line. When we find a point that is not on the line, we can create a new line between any point on the line and the new point. This defines a new 1-dimensional space (a line) for every point on the original line, all of these new lines pass through the new point.

Since there are an infinite number of points on the original line, we see that there are an infinite number of 1-dimensional lines that can be drawn through the new point all in different directions. The space formed by this infinite number of lines is called a 2-dimensional space. It is called 2-dimensional due to the “language” necessary to describe the location of any point in this space. To locate any point, we must choose a reference point, then first (1) we need to choose one of the lines passing through the reference point, and second (2) we use the methods we have already discussed to determine the location of a point along this reference line. Thus, the location of a point thus requires 2 numbers, one (1) to locate the reference line, and the other (2) to determine the location of the point along this line.

The concept of point symmetry in 2-dimensional spaces also comes into play. It means that measuring distances is the same in every direction. This invariance of direction means that if we have a “ruler” that measures a distance along any of the lines in this space, and we change the direction of the ruler, the length of the ruler does not change.

Imagine how the world would look if measuring lengths in one direction were different than lengths in another direction. If the invariance of direction was not true, then when we changed direction, the distance between things would shorten or lengthen, depending on which direction we faced. This is not what we experience in real life.

We can use the same concepts that we used to extend 1-dimensional space to 2-dimensional space to extend into spaces into any number of dimensions. How many distinct points do you need to generate a 3-dimensional space? Think about it. We will discuss how it can be done later.

Standard

Math Moments – The power of symmetry

If we were to consider any two points in the universe (A and C) and draw an imaginary line segment between these two points, there would be only one singular point on that line segment that preserves symmetry (under reflection). This is the midpoint (B) on the line segment which is exactly the same distance from each of the endpoints. You can reflect (flip) either one of the endpoints through the midpoint and it would fall exactly on the other endpoint. Such symmetry applies to all points on the line segment that are the same distance from this midpoint.

If you were to pick the midpoint as the reference point and the positive direction pointing toward one of the endpoints, then from the midpoint, the line segment in the positive direction looks exactly the same as the line segment in the negative direction. You could conceptually switch the positive direction with the negative direction, and nothing would change. This is called reflection symmetry, for obvious reasons.

If you have reflection symmetry, then anything that exists at a certain distance along the positive direction, also exists at that same distance in the negative direction; just like looking at things through a mirror. We use such symmetries in atomic physics all the time to make things easier.

For example, the electric field between two identical electrons, as observed from the midpoint between them, looks exactly the same when you are facing one electron as it does when you are facing the other. From the midpoint, everything is exactly the same in both directions, you cannot tell the difference between the electrons nor any of their physical properties from this perspective. To tell the difference, you would need to “break the symmetry” by introducing something else that is not symmetric to the midpoint.

So, once you have seen what exists on one side of the “mirror” we also know what will exist on the other side. It makes the math (and the diagrams) so much easier. We always should seek out these points of symmetry when we are doing the math, it makes everything so much more…symmetric.

Standard

Math Moments – The Number Line

Let’s imagine that you have a universe with only two points in it. You now draw a line segment between the two points and choose one of them to be the reference point. The location of any point along the line segment is now determined by the distance it is from the reference point. Now make a third point on the line segment that is exactly half-way between the two points. This new point is located at exactly half of the distance between the two end points.


Can you see the symmetry that is formed by these three points? The distance from the center point to either of the two end points is exactly the same. If you now were to choose the center point to be the reference point, then both end points would be the same distance away, but in opposite directions.


You would now need more than just the distance measurement alone to determine the location of points along the line. With three points, now direction becomes important. Again, using the axiom of choice and can choose which direction from the center point is positive, and which direction is negative.


We can then, finally, determine the location of every point on the line by specifying both a distance and a direction (positive or negative) from the center point. This arrangement of determining the locations of points on a line is called a “number line”. We call the distance and direction of each point on the line the Point’s coordinates. A Point’s coordinates uniquely determine its location on the line. Finally, we have a way of determining the location of a Point.


The center point is a special point of symmetry between the two endpoints. We can “rotate” the direction (exchange negative for positive directions) and the location (distance and direction) of the two identical endpoints would be exactly the same. This is called “rotational symmetry”. It means you can switch reference directions and the list of all the point coordinates will be the same. Remember that since you can’t tell the difference between points, the order of the list of points is not important.


Please believe me, taking the time to understand these concepts makes math so much more fun and easier later on. Learning these concepts is like learning the basic vocabulary of the math language.

Standard

Math Moments – 1-Dimensional Space

How can the exact location of the Point be described? This is a conceptual problem. It is also where some very advanced concepts of math (found in calculus and number theory) come to play. After some thought, it becomes obvious that if there was just one point in the universe, all by itself, it does not have an absolute location until you look at where it is relative to another point in the universe.


If there were only two points in the universe you could imagine a line segment drawn between the two points, and then there is some distance between the two points, you could pick one of the points as the reference point. Then you could describe the location of the second point as being a certain distance from the reference point. You only need one (1) distance measurement from the reference point to describe the location of the Point. This is why such a line is called 1-dimensional space.


You have now discovered quite a few interesting concepts, including the concept of the number “2”. Two identical objects in space that are distinguished by the distance between them. You have also discovered the concept of the number “1”, the concept of distance, and you are also starting to realize why Einstein’s theory is called the theory of relativity. Distances and times are only measurable relative to a reference point, and you can pick any of the points to be the reference point.


The idea that you can pick any of the points to be the reference point is called the axiom of choice. An axiom is something that is assumed to be true even though it has no definite proof. The axiom of choice forms the conceptual foundation for all mathematics.


Another concept that comes from using the distance from a reference point to describe location is the idea of symmetry. You can exchange the locations of two points, and you have not changed anything. It is impossible to tell the two points apart, and both points still have the same locations relative to every other point. This is called exchange symmetry. Symmetries makes math and physics much easier.

Standard