Alright, this is where it starts getting really interesting. We started out saying that we can use the language of math to build universes, at least in our imagination. We started out with (1) one point in the whole universe. Since a point has no size, the whole universe was simply a 0-dimensional space (a bit mind blowing).

After thinking about nothing for a while, we then thought about having (2) two points in the universe. We argued the concept of distance between these two points. We imagined two distinct completely identical points separated by a distance, this is the origin of the concept of the number 2. We then discussed a way to build a whole 1-dimensional space of points, a line between the two points.

We said that we could fill in the points on a line between these two points by first creating a midpoint a distance half-way between these points then, including the midpoint, use the same concept to create more new points in the middle of these points, and so on forever filling in the gaps (a bit more mind blowing).

We realized that there are an infinite number of points that can fit between our original 2 points, each of them described by the distance and direction they are from the midpoint. We started finding other points to fill in all the gaps between points.

We introduced the concept of symmetry; for every point on the line, everything must look exactly the same in both directions. This symmetry concept required that every point on the line has the same arrangement of points in either direction. If we ever found a point where the line ends, we could just add another segment onto the empty direction and keep doing this forever. This complete infinite 1-dimensional space of points is called a “line” (oh, the things we can think).

We named the two directions in this 1-dimensional space to be “negative” and “positive”. We can now choose any of the points to be a reference point and describe the position of any point in this space by its distance and direction from the reference point. We have thus introduced the number line.

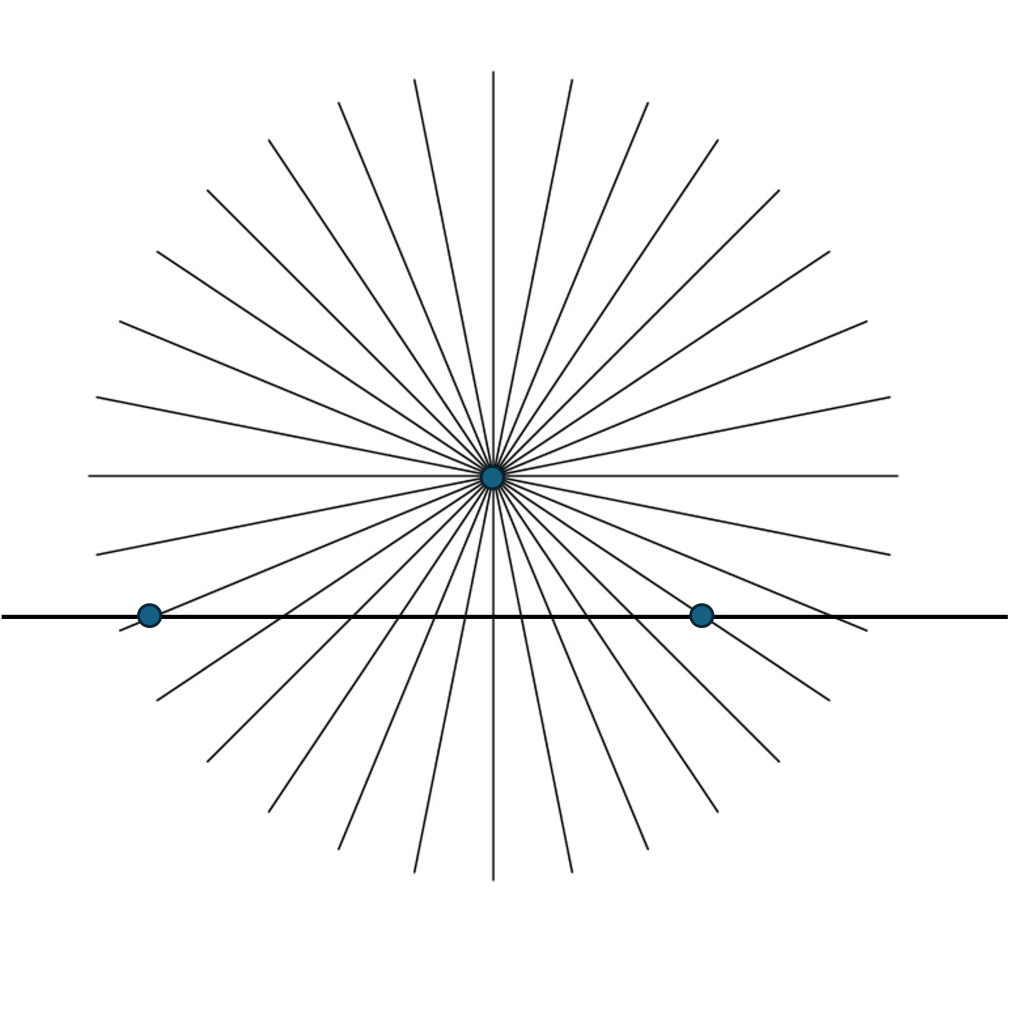
I hope you enjoyed this line of reasoning so far. We can now use the same line of reasoning we used to expand 0-dimensional space into 1-dimensional space in order to expand a 1-dimensional space into a 2-dimensional space.
As before, we only need to take the points we have in a 1-D space, on the line, and introduce another new point that is not in that space, not on the line. With this new point, we can now define another line by using this new point and any of the points on the original line to create a new line going in a different direction.

Since we can now create a distinct new line through the new point for every point on the original line, we have created an infinite array of new lines (1-D spaces) going off in different directions. Since the points on the original line can be infinitesimally close together, so are the lines. We include all the points on all these lines as part of a new 2-D space. We now have lots of points to connect together to form new lines. All these lines are said to live in this new 2-D space. An ancient mathematician, Euclid, studied these spaces, in honor of him, these “flat” spaces, of straight and parallel lines are called Euclidean spaces.

There are still some gaps. For example, there is a line that passes through the new point that is not connected to the original line, this line is said to be “parallel” to the original line, and since it never can cross the original line, it does not contain any of the points of the original line. As it turns out, building parallel lines using the tools we have requires a bit of doing.

So far, we have been exploring a 1-dimensional “space” of points along an infinitesimally thin line. Mathematicians call this a 1-dimentional space. The concept of symmetry implies that the line looks exactly the same in both directions. Therefore, this line must extend on forever in both directions, there is no point on the line where it ends. The line looks exactly the same on both sides of every point.

The concept of point symmetry in 1-dimensional space also means that if you were to reverse the direction of the “ruler” that measures the distance between any two points in this space, you will still measure the same distance between the points. This concept of invariance of direction is one of the most important characteristics of space. Of course, we need a lot more than just one line to describe all the space around us.

In order to expand the dimensions of space beyond this 1-dimensional space, we must assume that there is some point that is not in this space, a point that is not on the line. When we find a point that is not on the line, we can create a new line between any point on the line and the new point. This defines a new 1-dimensional space (a line) for every point on the original line, all of these new lines pass through the new point.

Since there are an infinite number of points on the original line, we see that there are an infinite number of 1-dimensional lines that can be drawn through the new point all in different directions. The space formed by this infinite number of lines is called a 2-dimensional space. It is called 2-dimensional due to the “language” necessary to describe the location of any point in this space. To locate any point, we must choose a reference point, then first (1) we need to choose one of the lines passing through the reference point, and second (2) we use the methods we have already discussed to determine the location of a point along this reference line. Thus, the location of a point thus requires 2 numbers, one (1) to locate the reference line, and the other (2) to determine the location of the point along this line.

The concept of point symmetry in 2-dimensional spaces also comes into play. It means that measuring distances is the same in every direction. This invariance of direction means that if we have a “ruler” that measures a distance along any of the lines in this space, and we change the direction of the ruler, the length of the ruler does not change.

Imagine how the world would look if measuring lengths in one direction were different than lengths in another direction. If the invariance of direction was not true, then when we changed direction, the distance between things would shorten or lengthen, depending on which direction we faced. This is not what we experience in real life.

We can use the same concepts that we used to extend 1-dimensional space to 2-dimensional space to extend into spaces into any number of dimensions. How many distinct points do you need to generate a 3-dimensional space? Think about it. We will discuss how it can be done later.